WWW und Mathematik — Lehren und Lernen im Internet
WWW und Mathematik — Lehren und Lernen im Internet
WWW und Mathematik — Lehren und Lernen im Internet
Erfolgreiche ePaper selbst erstellen
Machen Sie aus Ihren PDF Publikationen ein blätterbares Flipbook mit unserer einzigartigen Google optimierten e-Paper Software.
Ingmar Lehmann<br />
Auch dieser Abstand a zwischen beiden<br />
Quadraten ist somit unabhängig von der Seitenlänge<br />
des Ausgangsquadrates. Das gilt<br />
damit auch für ein Quadrat mit der Seitenlänge<br />
von 10 000 km.<br />
Die Verlängerung um 1 m erzeugt daher<br />
auch in diesem <strong>—</strong> dem Äquator nachempf<strong>und</strong>enen<br />
<strong>—</strong> Beispiel einen Abstand von<br />
12,5 cm. Hier erscheint das Ergebnis "glaubhafter"<br />
als die 16 cm (für das Seil um den<br />
Äquator), da man ja "sieht", wo die Verlängerung<br />
um 1 m bleibt!<br />
Anstelle eines Quadrates kann man auch ein<br />
gleichseitiges Dreieck, allgemein ein regelmäßiges<br />
Vieleck, betrachten <strong>und</strong> nach dem<br />
Abstand des Fadens vom Vielecksrand fragen.<br />
Aufgabe 7: Ein Seil um ein regelmäßiges<br />
n-Eck<br />
Um ein regelmäßiges n-Eck wird ein Fadenn-Eck<br />
gespannt, das um 1 m länger ist als<br />
der Umfang des gegebenen n-Ecks.<br />
Der Faden wird dabei so gespannt, dass die<br />
jeweiligen n-Eckseiten zueinander parallel<br />
sind (vgl. Abb. 6, 7, 8).<br />
Welchen Abstand a hat der Faden vom Rand<br />
des Ausgangs-n-Ecks? Genauer: Welchen<br />
Abstand a haben die jeweiligen zueinander<br />
parallelen n-Eck-Seiten?<br />
Lösung: (<strong>im</strong> Überblick)<br />
Auch für die drei regelmäßigen Vielecke in<br />
Abb. 6, 7, 8 ist also der Abstand a zwischen<br />
den jeweiligen zueinander parallelen Vieleckseiten<br />
unabhängig von der Seitenlänge<br />
des Ausgangsvielecks.<br />
Für ein beliebiges regelmäßiges n-Eck gilt<br />
mit n·s+1 = n·s+2·n·b dann 1 = 2·n·b; mit<br />
π<br />
cot<br />
π b 1<br />
tan = folgt damit a = = n .<br />
n a<br />
π 2n<br />
2n<br />
tan<br />
n<br />
Je größer die Eckenzahl n ist, umso größer<br />
wird der Abstand a. Wächst a beliebig?<br />
Natürlich kann dieser Abstand a niemals<br />
größer werden als der <strong>im</strong> Falle des Kreises!<br />
Der Abstand a liegt <strong>im</strong> Falle des regelmäßigen<br />
Sechsecks (14,4 cm) schon relativ nahe<br />
an dem Grenzwert, den wir in Aufgabe 1<br />
gewonnen haben (≈16 cm):<br />
a = l<strong>im</strong><br />
n→∞<br />
130<br />
1 1<br />
= ≈16 [cm].<br />
π<br />
2n<br />
tan<br />
2π<br />
n<br />
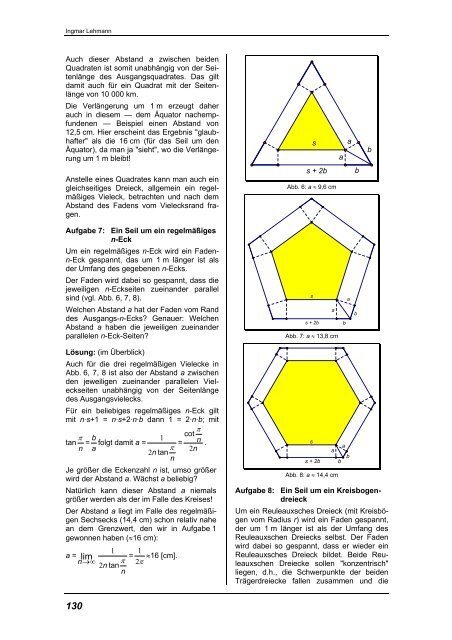
s<br />
s + 2b<br />
Abb. 6: a ≈ 9,6 cm<br />
s<br />
s + 2b<br />
a<br />
Abb. 7: a ≈ 13,8 cm<br />
s<br />
s + 2b<br />
a<br />
Abb. 8: a ≈ 14,4 cm<br />
Aufgabe 8: Ein Seil um ein Kreisbogendreieck<br />
Um ein Reuleauxsches Dreieck (mit Kreisbögen<br />
vom Radius r) wird ein Faden gespannt,<br />
der um 1 m länger ist als der Umfang des<br />
Reuleauxschen Dreiecks selbst. Der Faden<br />
wird dabei so gespannt, dass er wieder ein<br />
Reuleauxsches Dreieck bildet. Beide Reuleauxschen<br />
Dreiecke sollen "konzentrisch"<br />
liegen, d.h., die Schwerpunkte der beiden<br />
Trägerdreiecke fallen zusammen <strong>und</strong> die<br />
a<br />
b<br />
b<br />
a<br />
a<br />
a<br />
b<br />
b<br />
b<br />
b