- Seite 5 und 6:
Einführung in die höhere Mathemat
- Seite 7 und 8:
GELEITWORT DES HERAUSGEBERS Für di
- Seite 9 und 10:
Geleitwort des Herausgebers IX Das
- Seite 11 und 12:
Vorwort des Verfassers XI werter al
- Seite 13 und 14:
INHALT I.Teil. Funktionen einer Ver
- Seite 15:
Inhalt 3. Kapitel. Graphische, nume
- Seite 18 und 19:
4 I. Teil. Funktionen einer Veränd
- Seite 20 und 21:
6 1. Teil. Funktionen einer Veränd
- Seite 22 und 23:
8 I. Teil. Funktionen einer Veränd
- Seite 25 und 26:
2. Darstellung von Funktionen 11 tr
- Seite 27 und 28:
2. Darstellung von Funktionen 13 Un
- Seite 29 und 30:
2. Darstellung von Funktionen 15 te
- Seite 31 und 32:
2. Darstellung von F u n k t i o n
- Seite 33 und 34:
2. Darstellung von Funktionen 19 De
- Seite 35 und 36:
2. KAPITEL Die wichtigsten Funktion
- Seite 37 und 38:
3. Die Konstante 23 Temperatur. Inf
- Seite 39 und 40:
3. Die Konstante 25 lauft die Gerad
- Seite 41 und 42:
4. Die Proportionalität 27 die Me
- Seite 43 und 44:
6. Die lineare Funktion 29 Eine bes
- Seite 45 und 46:
im b red , t-System darzustellen. W
- Seite 47 und 48:
6. Die Parabeln y = x n 33 6. Die P
- Seite 49 und 50:
7. Der Begriff des Differentialquot
- Seite 51 und 52:
7. Der Begriff des Differentialquot
- Seite 53 und 54:
1. Der Begriff des Differentialquot
- Seite 55 und 56:
tion. 7. Der Begriff des Differerit
- Seite 57 und 58:
8. Einige Differentiationsregeln 43
- Seite 59 und 60:
8. Einige Differentiationsregeln 45
- Seite 61 und 62:
Im angenommenen Beispiel ist 9. Das
- Seite 63 und 64:
9. Das Differential 4y Es ist aber
- Seite 65 und 66:
10. Umkehrfunktionen und Umkehrrege
- Seite 67 und 68:
10. Umkehrfunktionen und Umkehrrege
- Seite 69 und 70:
11. Die Funktionen vom Typus 55 II.
- Seite 71 und 72:
11. Die Funktionen vom Typus 57 Wie
- Seite 73 und 74:
11. Die Funktionen vom Typus 59 son
- Seite 75 und 76:
11. Die Funktionen vom Typus 61 lum
- Seite 77 und 78:
11. Die Funktionen vom Typus 63 bin
- Seite 79 und 80:
12. Die Kettenregel 65 tiationsrege
- Seite 81 und 82:
12. Die Kettenregel G7 Kurve III) d
- Seite 83 und 84:
12. Die Kettenregel 69 Damit wird D
- Seite 85 und 86:
13. Extremwert- und Wendepunktsbest
- Seite 87 und 88:
13. Extremwert- und Wendepunktsbest
- Seite 89 und 90:
13 Extremwert- und Wendepunktsbesti
- Seite 91 und 92:
Die Funktion 13. Extremwert- und We
- Seite 93 und 94:
13. Extremwert- und Wendepunktsbest
- Seite 95 und 96:
13, Extremwert- und Wendepunktsbest
- Seite 97 und 98:
und daher ist 13. Extremwert- und W
- Seite 99 und 100:
13. Extremwert- und Wendepunktsbest
- Seite 101 und 102:
13. Extremwert- und Wendepunktsbest
- Seite 103 und 104:
13. Extremwert- und Wendepunktsbest
- Seite 105 und 106:
Ist diese festgelegt, dann ist auch
- Seite 107 und 108:
15. Darstellung und Differentiation
- Seite 109 und 110:
.15. Darstellung und Differentiatio
- Seite 111 und 112:
15. Darstellung und Differentiation
- Seite 113 und 114:
16. Logarithmische Papiere 99 logar
- Seite 115 und 116:
16. Logarithmische Papiere 101 Auch
- Seite 117 und 118:
16. Logarithmische Papiere 103 nate
- Seite 119 und 120:
16. Logarithmische Papiere 105 Man
- Seite 121 und 122:
16. Logarithmische Papiere 107 Beso
- Seite 123 und 124:
17. Der logarithmische Rechenschieb
- Seite 125 und 126:
17. Der logarithmische Rechenschieb
- Seite 127 und 128:
17. Der logarithmische Rechenschieb
- Seite 129 und 130:
17. Der logarithmische Rechenschieb
- Seite 131 und 132:
17. Der logarithmische Rechenschieb
- Seite 133 und 134:
18. Darstellung und Differentiation
- Seite 135 und 136:
X 0.00 0,01 0,02 0,03 0,04 0,05 0,0
- Seite 137 und 138:
19. Produkt- und Quotientenregel 12
- Seite 139 und 140:
19. Produkt- und Quotientenregel 12
- Seite 141 und 142:
19. Produkt- und Quotientenregel 12
- Seite 143 und 144:
20. Die negative Exponentialfunktio
- Seite 145 und 146:
20. Die negative Exponentialfunktio
- Seite 147 und 148:
20. Die negative Exponentialfunktio
- Seite 149 und 150:
20. Die negative Exponentialfunktio
- Seite 151 und 152:
20. Die negative Exponentialfunktio
- Seite 153 und 154:
21. Die Funktion y = e x 139 21. Di
- Seite 155 und 156:
21. Die Funktion 141 Die ganze Kurv
- Seite 157 und 158:
21. Die Funktion 143 Kubikzentimete
- Seite 159 und 160:
21. Die Funktion 145 Tabelle 9 Temp
- Seite 161 und 162:
22. Die Funktionen 147 besteht. Ent
- Seite 163 und 164:
22. Die Funktionen 149 ist eine Kon
- Seite 165 und 166:
22. Die Funktionen 151 Bei der allg
- Seite 167 und 168:
22. Die Funktionen 153 Wie sieht nu
- Seite 169 und 170:
22. Die Funktionen 155 Der Ausdruck
- Seite 171 und 172:
23. Die Hyperbelfunktionen 157 sulf
- Seite 173 und 174:
23. Die Hyperbelfunktionen 159 Ganz
- Seite 175 und 176:
24. Darstellung und Differentiation
- Seite 177 und 178:
erhalten wir 24. Darstellung und Di
- Seite 179 und 180:
25. Zyklometrische Funktionen als U
- Seite 181 und 182:
3. KAPITEL Näherungsverfahren zur
- Seite 183 und 184:
Näherungsverfahren zw Auflösung v
- Seite 185 und 186:
26. Das Newtonsche Näherungsverfah
- Seite 187 und 188:
26. Das Newtonsche Näherungsverfah
- Seite 189 und 190:
27. Das Iterationsverfahren 175 So
- Seite 191 und 192:
27. Das Iterationsverfahren 177 Tab
- Seite 193 und 194: 4. KAPITEL Reihendarstellung von Fu
- Seite 195 und 196: 28. Der Begriff der Potenzreihe 181
- Seite 197 und 198: 28. Der Begriff der Potenzreihe 183
- Seite 199 und 200: 29. Die MacLaurin-Reihe 185 So lass
- Seite 201 und 202: 30. Die Taylor-Reihe 187 sogenannte
- Seite 203 und 204: 32. Das Rechnen mit Reihen 189 dies
- Seite 205 und 206: 32. Das Rechnen mit Reihen 191 Wir
- Seite 207 und 208: 33. Die binomische Reihe und das Re
- Seite 209 und 210: 33. Die binomische Reihe und das Re
- Seite 211 und 212: 33. Die binomische Reihe und das Re
- Seite 213 und 214: 5. KAPITEL Unbestimmte Ausdrücke 3
- Seite 215 und 216: 34. Der Begriff des unbestimmten Au
- Seite 217 und 218: 35. Auswertung unbestimmter Ausdrü
- Seite 219 und 220: 35. Auswertung unbestimmter Ausdrü
- Seite 221: 36. Auswertung unbestimmter Ausdrü
- Seite 225 und 226: 1. KAPITEL Allgemeines über Differ
- Seite 227 und 228: 36. Etwas über Differentialgleichu
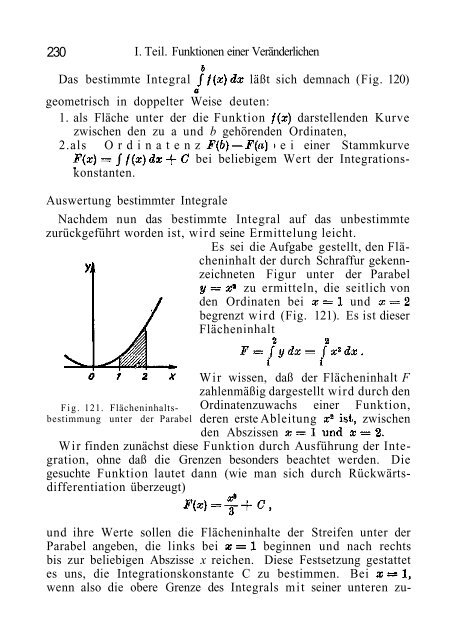
- Seite 229 und 230: 36. Etwas über Differentialgleichu
- Seite 231 und 232: 37. Das unbestimmte Integral 217 su
- Seite 233 und 234: 37. Bas unbestimmte Integral 219 Ma
- Seite 235 und 236: 37. Das unbestimmte Integral 221 un
- Seite 237 und 238: 38. Bestimmtes Integral und sein Zu
- Seite 239 und 240: 38. Bestimmtes Integral und sein Zu
- Seite 241 und 242: 38. Bestimmtes Integral und sein Zu
- Seite 243: 38. Bestimmtes Integral und sein Zu
- Seite 247 und 248: 38. Bestimmtes Integral und sein Zu
- Seite 249 und 250: 38. Bestimmtes Integral und sein Zu
- Seite 251 und 252: 38. Bestimmtes Integral und sein Zu
- Seite 253 und 254: 2. KAPITEL Integrationsmethoden Beg
- Seite 255 und 256: 39. Grundintegrale 241 Es sei zu in
- Seite 257 und 258: 39. Grundintegrale 243 Zur Durchfü
- Seite 259 und 260: 39. Grundintegrale 245 portional de
- Seite 261 und 262: 39. Grundintegrale 247 Damit erhalt
- Seite 263 und 264: 40. Die Substitutionsmethode 249 Al
- Seite 265 und 266: also mathematisch ausgedrückt, ist
- Seite 267 und 268: 40. Die Substitutionsmethode 253 ge
- Seite 269 und 270: 40. Die Substitutionsmethode 255 Ma
- Seite 271 und 272: 4L Partielle Integration 257 Das zw
- Seite 273 und 274: 41. Partielle Integration 259 Die B
- Seite 275 und 276: 41. Partielle Integration 261 Die L
- Seite 277 und 278: 4L Partielle Integration 263 Mit di
- Seite 279 und 280: 42. Integration durch Partialbruchz
- Seite 281 und 282: 42. Integration durch Partialbruchz
- Seite 283 und 284: 42. Integration durch Partialbruchz
- Seite 285 und 286: 43. Näherungsweise Auswertung von
- Seite 287 und 288: 43. Näherungsweise Auswertung von
- Seite 289 und 290: 43. Näherungsweise Auswertung von
- Seite 291 und 292: 3. KAPITEL Graphische, numerische u
- Seite 293 und 294: 44. Mechanische Methoden zur Auswer
- Seite 295 und 296:
44. Mechanische Methoden zur Auswer
- Seite 297 und 298:
45. Numerische Näherungsmethoden z
- Seite 299 und 300:
45. Numerische Näherungsmethoden z
- Seite 301 und 302:
45. Numerische Näherungsmethoden z
- Seite 303 und 304:
45. Numerische Näherungsmethoden z
- Seite 305 und 306:
46. Ermittelung der Stammfunktion u
- Seite 307 und 308:
46. Ermittelung der Stammfunktion u
- Seite 309 und 310:
47. Ermittelung der Stammfunktion d
- Seite 311:
47. Ermittelung der Stammfunktion d
- Seite 315 und 316:
1. KAPITEL Darstellung von Funktion
- Seite 317 und 318:
48. Analytische und tabellarische D
- Seite 319 und 320:
49. Geometrische Darstellung usw. 3
- Seite 321 und 322:
49. Geometrische Darstellung usw. 3
- Seite 323 und 324:
49. Geometrische Darstellung usw. 3
- Seite 325 und 326:
50. Darstellung durch eine Netztafe
- Seite 327 und 328:
50. Darstellung durch eine Netztafe
- Seite 329 und 330:
60. Darstellung durch eine Netztafe
- Seite 331 und 332:
51. Darstellung durch eine Fluchtli
- Seite 333 und 334:
51. Darstellung durch eine Fluchtli
- Seite 335 und 336:
51. Darstellung durch eine Fluchtli
- Seite 337 und 338:
51., Darstellung durch eine Fluchtl
- Seite 339 und 340:
51. Darstellung durch eine Fluchtli
- Seite 341 und 342:
61. Darstellung durch eine Fluchtli
- Seite 343 und 344:
öl. Darstellung durch eine Fluchtl
- Seite 345 und 346:
2. KAPITEL Differentiation 62. Part
- Seite 347 und 348:
52. Partielle Differentiation und d
- Seite 349 und 350:
52. Partielle Differentiation und d
- Seite 351 und 352:
52. Partielle Differentiation and d
- Seite 353 und 354:
52. Partielle Differentiation und d
- Seite 355 und 356:
52. Partielle Differentiation und d
- Seite 357 und 358:
53. Höhere partielle Differentialq
- Seite 359 und 360:
63. Höhere partielle Differentialq
- Seite 361 und 362:
54. Ermittelung von Extremwerten 34
- Seite 363 und 364:
55. Ausgleichsrechnung nach der Met
- Seite 365 und 366:
55. Ausgleichsrechnung nach der Met
- Seite 367 und 368:
55. Ausgleichsrechnung nach der Met
- Seite 369 und 370:
3. KAPITEL Integration 56. Das voll
- Seite 371 und 372:
56. Das vollständige und das unvol
- Seite 373 und 374:
56. Das vollständige und das unvol
- Seite 375 und 376:
57. Integration eines vollständige
- Seite 377 und 378:
57. Integration eines vollständige
- Seite 379 und 380:
57. Integration eines vollständige
- Seite 381 und 382:
58. Integration eines unvollständi
- Seite 383 und 384:
58. Integration eines unvollständi
- Seite 385 und 386:
58. Integration eines unvollständi
- Seite 387 und 388:
58. Integration eines unvollständi
- Seite 395:
Anhang 381 Ermittle den Wert des be
- Seite 406 und 407:
392 Sach- und Namenregister Carnots
- Seite 408 und 409:
394 Sach- und Namenregister Funktio
- Seite 410 und 411:
396 Sach- und Namenregister kinetis
- Seite 412 und 413:
398 Sach- und Namenregister Polabst
- Seite 414:
400 Sach- und Namenregister Veränd