- Seite 1:
Φ Φ Φ Φ Φ Φ Φ Φ Φ Φ Φ Φ
- Seite 5 und 6:
Inhaltsverzeichnis 0 Einleitung 1 0
- Seite 7 und 8:
Inhaltsverzeichnis 3.2.1 Mathematis
- Seite 9 und 10:
Inhaltsverzeichnis 5.2.3 Poisson-Th
- Seite 11 und 12:
Inhaltsverzeichnis vii
- Seite 13 und 14:
0 Einleitung 0.1 Vorbemerkung Diese
- Seite 15 und 16:
1 Vektorrechnung 1.1 Grunddefinitio
- Seite 17 und 18:
a b a + b b 1.2 Vektoroperationen A
- Seite 19 und 20: a b φ a b 1.2 Vektoroperationen Ab
- Seite 21 und 22: 1.3 Komponentendarstellung von Vekt
- Seite 23 und 24: 1.3 Komponentendarstellung von Vekt
- Seite 25 und 26: (A1.4.1) Beweisen Sie die Identitä
- Seite 27 und 28: 1.6 Anwendungen der Vektorrechnung
- Seite 29 und 30: 1.7 Differentiation und Integration
- Seite 31 und 32: 1.7.2 Integration von Vektoren 1.8
- Seite 33 und 34: x z φ z r Abbildung 1.12: Zur Einf
- Seite 35 und 36: (ρ cos φ, ρ sin φ, z). Mit Glei
- Seite 37 und 38: is zur ersten Ordnung ergibt: dψ =
- Seite 39 und 40: 1. auf eine skalare Funktion T (�
- Seite 41 und 42: 1.9.4 Rotation 1.9 Vektorielle Diff
- Seite 43 und 44: jeweils zwei für Gradienten, Diver
- Seite 45 und 46: Einheitsvektoren mit dem Skalenfakt
- Seite 47 und 48: 1.11 Differentialoperatoren in krum
- Seite 49 und 50: 1.11.6 Beispiel: Kugelkoordinaten M
- Seite 51 und 52: 2 Newtonsche Mechanik Die klassisch
- Seite 53 und 54: 2.1 Das Physikalische Weltbild vor
- Seite 55 und 56: 2.1 Das Physikalische Weltbild vor
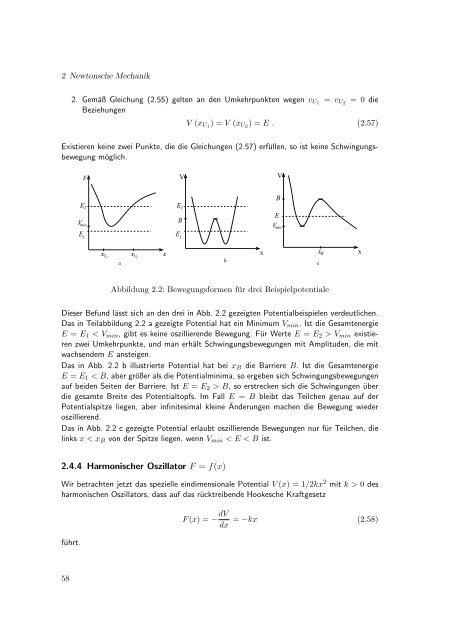
- Seite 57 und 58: 2.2 Die Newtonschen Axiome einen Or
- Seite 59 und 60: 2.2 Die Newtonschen Axiome Newton p
- Seite 61 und 62: 2.2 Die Newtonschen Axiome allein i
- Seite 63 und 64: 2.3.2 Arbeit 2.3 Grundbegriffe der
- Seite 65 und 66: Für die elastische Kraft 2.3 Grund
- Seite 67 und 68: 2.4 Integration der Bewegungsgleich
- Seite 69: 2.4.3 Konservatives Kraftfeld F = f
- Seite 73 und 74: 2.4 Integration der Bewegungsgleich
- Seite 75 und 76: 2.5 Reibung Die Wurfdauer ergibt si
- Seite 77 und 78: und durch direkte Integration � t
- Seite 79 und 80: 3 Analytische Mechanik 3.1 Eingesch
- Seite 81 und 82: m Z l y φ K= mge 2 Abbildung 3.2:
- Seite 83 und 84: 3.2 Beispiel 2: Das Pendel im Schwe
- Seite 85 und 86: 3.2 Beispiel 2: Das Pendel im Schwe
- Seite 87 und 88: 3.3 Beschreibung von Flächen und K
- Seite 89 und 90: 3.4.1 Wieder Beispiel 1: Schiefe Eb
- Seite 91 und 92: 3.4.2 Allgemeiner Fall 3.4 Lagrange
- Seite 93 und 94: 3.5 Energieerhaltungssatz im Fall v
- Seite 95 und 96: 3.6 Das Prinzip von d’Alembert (b
- Seite 97 und 98: 3.7 Lagrange-Gleichungen 2. Art Mul
- Seite 99 und 100: 3.7 Lagrange-Gleichungen 2. Art Ein
- Seite 101 und 102: 3.8.2 Atwoodsche Fallmaschine 3.8 E
- Seite 103 und 104: so sind die Koeffizienten (3.101) u
- Seite 105 und 106: l + l 1 2 folgt für die kinetische
- Seite 107 und 108: 3.9 Weitere Anwendungen dessen Lös
- Seite 109 und 110: 3.10.1 Beispiele x 1 y (x) 3.10 Exk
- Seite 111 und 112: α = 0 liefert den Extremalwert J(
- Seite 113 und 114: 3.10 Exkurs über Variationsprinzip
- Seite 115 und 116: Setzen wir dies in Gleichung (3.148
- Seite 117 und 118: 3.11 Hamiltonsches Prinzip Weil die
- Seite 119 und 120: Durch Aufsummieren folgt sowohl als
- Seite 121 und 122:
x R Θ l φ 3.11 Hamiltonsches Prin
- Seite 123 und 124:
3.12 Symmetrien und Erhaltungssätz
- Seite 125 und 126:
3.12 Symmetrien und Erhaltungssätz
- Seite 127 und 128:
3.12 Symmetrien und Erhaltungssätz
- Seite 129 und 130:
y r y’ K K’ V r’ 3.12 Symmetr
- Seite 131 und 132:
3.12 Symmetrien und Erhaltungssätz
- Seite 133 und 134:
3.12.5 Noether-Theorem für autonom
- Seite 135 und 136:
3.13 Geschwindigkeitsabhängige Kr
- Seite 137 und 138:
Weil � A(�r, t) nicht von der G
- Seite 139 und 140:
Es ist �vi · ∂�vi ∂ ˙ qj
- Seite 141 und 142:
so dass wir den Virial-Satz erhalte
- Seite 143 und 144:
4 Das Zweikörper-Problem Wir betra
- Seite 145 und 146:
4.2 Relativbewegung schreiben könn
- Seite 147 und 148:
wir mit Gleichung (4.19) für die
- Seite 149 und 150:
Durch Integration erhalten wir r mi
- Seite 151 und 152:
4.3 Kepler-Problem: Planetenbewegun
- Seite 153 und 154:
4.4 Mathematische Zwischenbetrachtu
- Seite 155 und 156:
4.4 Mathematische Zwischenbetrachtu
- Seite 157 und 158:
4.4 Mathematische Zwischenbetrachtu
- Seite 159 und 160:
4.5 Fortsetzung des Kepler-Problems
- Seite 161 und 162:
4.5 Fortsetzung des Kepler-Problems
- Seite 163 und 164:
a b ψ c = aε 4.5 Fortsetzung des
- Seite 165 und 166:
4.5 Fortsetzung des Kepler-Problems
- Seite 167 und 168:
4.6 Hyperbelbahnen f(φ) kann das V
- Seite 169 und 170:
Aphel rmax rmin m1 Perihel Abbildun
- Seite 171 und 172:
4.8 Das Streuproblem des Targetteil
- Seite 173 und 174:
Benutzen wir Θ = π − 2φG , so
- Seite 175 und 176:
5 Hamilton-Mechanik Mit der Hamilto
- Seite 177 und 178:
5.1 Hamiltonsche Bewegungsgleichung
- Seite 179 und 180:
p Amω A A 5.1 Hamiltonsche Bewegun
- Seite 181 und 182:
π 2 p φ 5.1 Hamiltonsche Bewegung
- Seite 183 und 184:
Definition : Wir definieren die Poi
- Seite 185 und 186:
Gleichung, so folgt d [f, g] = dt =
- Seite 187 und 188:
Aus den Gleichungen (5.52) und (5.5
- Seite 189 und 190:
5.3 Kanonische Transformationen wei
- Seite 191 und 192:
5.3 Kanonische Transformationen ver
- Seite 193 und 194:
5.4 Hamilton-Jacobi-Gleichung 5.4 H
- Seite 195 und 196:
5.4 Hamilton-Jacobi-Gleichung Das s
- Seite 197 und 198:
5.4 Hamilton-Jacobi-Gleichung (e) M
- Seite 199 und 200:
5.6 Separation der Variablen Die Ko
- Seite 201 und 202:
5.6 Separation der Variablen Die HJ
- Seite 203 und 204:
5.6.2 Beispiel: Teilchen im Schwere
- Seite 205 und 206:
5.7 Satz von Liouville Bezeichnen w
- Seite 207 und 208:
Satz von Poincare: Das Integral �
- Seite 209 und 210:
5.8 Integralinvarianten von Poincar
- Seite 211 und 212:
6 Bewegung des starren Körpers 6.1
- Seite 213 und 214:
x’ x z z’ y’ y 6.1 Kinematik
- Seite 215 und 216:
wobei ɛik infinitesimal klein sein
- Seite 217 und 218:
e 1 dφ d Ω e 3 x’ x Θ Θ Abbi
- Seite 219 und 220:
ω r K θ F Zentr. Abbildung 6.5: Z
- Seite 221 und 222:
6.4 Trägheitstensor und Hauptachse
- Seite 223 und 224:
6.4 Trägheitstensor und Hauptachse
- Seite 225 und 226:
O 6.4 Trägheitstensor und Hauptach
- Seite 227 und 228:
Mit �rα = � R + �r ′ α od
- Seite 229 und 230:
6.4.5 Hauptachsentransformation 6.4
- Seite 231 und 232:
6.5 Das Trägheitsellipsoid Setzen
- Seite 233 und 234:
6.6 Die Eulerschen Gleichungen mit
- Seite 235 und 236:
ω (ω ,ω ,0) 1 2 e 1 e 3 6.6 Die
- Seite 237 und 238:
6.7 Die Eulerschen Winkel 6.7 Die E
- Seite 239 und 240:
χ’ θ χ η’ ξ = ξ’ Abbild
- Seite 241 und 242:
6.8 Lagrange-Mechanik des starren K
- Seite 243 und 244:
Für den symmetrischen Kreisel ist
- Seite 245 und 246:
6.8 Lagrange-Mechanik des starren K
- Seite 247 und 248:
Aus der Lagrange-Funktion (6.119) f
- Seite 249 und 250:
7 Spezielle Relativitätstheorie Ei
- Seite 251 und 252:
7.1 Die Lorentz-Transformation Die
- Seite 253 und 254:
folgen mit den Gleichungen (7.23)
- Seite 255 und 256:
Zum einen gilt nach dem Transformat
- Seite 257 und 258:
7.2 Minkowski-Raum 7.2 Minkowski-Ra
- Seite 259 und 260:
7.3 Lagrange-Formulierung der relat
- Seite 261 und 262:
7.3 Lagrange-Formulierung der relat
- Seite 263 und 264:
8 Kosmologie fast ohne Allgemeine R
- Seite 265 und 266:
8.3 Dichte und Druck des Universums
- Seite 267 und 268:
8.3.4 Quintessenz 8.4 Vakuumdruck N
- Seite 269 und 270:
8.5.3 Vakuum Für das Vakuum erhalt
- Seite 271 und 272:
8.7 Zukünftige Beschleunigung des
- Seite 273 und 274:
8.8 Rotverschiebung, Lichtlaufzeit
- Seite 275 und 276:
Für Ωm0 < 1 gilt τ (r, Ωm0 <
- Seite 277 und 278:
A Anhang A.1 Mathematischer Anhang
- Seite 279:
A.2 Empfohlene Literatur A.2.1 Büc