U. Glaeser

Recommendations

Info

Impulse Response 0.2 0.15 0.1 0.05 0 0 10 20 30 40 50 Index (n) FIGURE 26.7 Digital filter design via Kaiser windowing: (a) shows the impulse response of an ideal lowpass filter (circles with dotted lines) and the filter designed by windowing (filled circles with solid lines). The windowed filter is the product of the ideal impulse response and the Kaiser window with β = 5 (dashed line); (b) shows the log magnitude of four filters designed using the Kaiser window with different parameters β. Frequency Sampling Another common, but naive, approach to FIR design is the method of frequency sampling. In this case, the ideal frequency response is sampled over the range −π < ω ≤ π at M + 1 points and then the inverse FFT is computed to get the order-M impulse response, which then contains the coefficients of the FIR filter. It is possible to let a few of the frequency samples be free parameters for a linear program that will optimize the resultant H(ω). This, in turn, improves the filter characteristics by making the error smaller near the cutoff frequency. Weighted Least-Squares Although frequency sampling filters and windowing designs have pretty good responses, neither one is an optimal filter. In the general optimization approach, the transition band of the frequency response should be treated as a “don’t care” region. For common frequency selective filters, the optimal filter will have a smooth behavior in the transition band even though no optimization is done in that “don’t care” region. The FIR filter can be designed by minimizing any norm with a guaranteed unique solution. The design can be generalized further by using a weighting function on the error. For example, the weight can be used in clever ways to control the error. Here is the weight definition for an inverse filter (or equalizer). The weighted design problem usually involves optimizing the norm of the error over the entire frequency domain, but that is done numerically by working on a dense frequency grid. The easiest optimization problem is the least-squares norm minimization because the partial derivatives (which are the elements of the gradient) of the least-squares norm with respect to the filter coefficients are all linear combinations of the filter coefficients. This property implies that the optimal filter can be found by solving the set of linear equations obtained by setting all those partial derivatives to zero. The solution for the weighted least-squares FIR filter is © 2001 by CRC Press LLC Windowed Impulse Response Kaiser(5.0) Window (scaled by 2*f c ) Log Magnitude (dB) LPFs with cutoff at ω = 0.1π 0 0.1π 0.2π 0.3π Frequency ( ω) (a) (b) I Eq(ω) 0 −30 −60 −90 Kaiser(0.0) Kaiser(3.0) Kaiser(5.0) Kaiser(8.0) D(ω) = ----------------- , W HSys(ω ) Eq(ω) = HSys(ω) W(ω) ∂ ------------- W( I– H) ∂b[ n] 2 ∫ dω = 0, ω for n = 0, 1,…,M W 2 Ie jωn ∫ ⎛ jω( n−k ) – ∑b[ k]e ⎞ dω = ⎝ ⎠ 0, for n = 0, 1,…,M ω k
For IIR filters, the problem is not nearly so easy because the denominator of the frequency response function makes the problem nonlinear. The solution can still be carried out by computing the partial derivatives and setting them equal to zero: The solution may not exist, however, but even if it does, it is often not unique. Furthermore, it is likely that only a locally optimal solution of the nonlinear equations can be found. Another approach is to use an iteration to find a close-to-optimal solution using the Steiglitz–McBride method [15]: The solution can be realized by iteratively updating the rational functions W/|A| and B/A. Remez Exchange Least-squares filters are not desirable in many applications because they exhibit large worst-case error near the transition band. On the other hand, the worst-case error can be minimized by reformulating the design problem as a Chebyshev (or min-max) problem. This min-max problem is usually difficult to solve unless the problem can be transformed into a real 1 problem. To do this, the ideal filter needs to be a linear-phase filter with a group delay of -- M. Then the 2 problem becomes an approximation of a real function by a sum of sinusoidal functions. For the special case of an even-order FIR filter with symmetric coefficients, the real problem becomes: 1 1 1 1 where a = [1] and b = [ -- cN/2,…, -- c1,c0, -- c1,…, -- cN/2]. This min-max problem can be solved by the Remez 2 2 2 2 algorithm [16–19]. The algorithm exploits the famous Alternation Theorem, which gives the necessary and sufficient condition for an optimal real Chebyshev solution as one that has at least M + 2 alternating extremal points (i.e., points where the error is maximal). The operation of the algorithm involves an exchange that iteratively updates the extremal set and solves for the alternating error on that set. It turns out that the Remez Exchange algorithm is very efficient and always converges, so it has become a classical method for FIR filter design as the Parks–McClellan algorithm. Linear Programming Filter design by optimizing the norm of the weighted error can be further improved by applying constraints. However, only the magnitude constrained problem seems to be easy to solve © 2001 by CRC Press LLC W A ∗ -------- I B ⎛ ⎛ – --- ⎞⎞ ∫ dω = 0, for n = 0,1,…,M ω ⎝ ⎝ A⎠⎠ 2 e jωn W A ∗ -------- B∗ A ∗ ----- I B ⎛ ⎛ – --- ⎞⎞ ∫ dω = 0, for n = 0,1,…,N ω ⎝ ⎝ A⎠⎠ 2 e jωn min W I B ⎛ – --- ⎞ min ⎝ A⎠ W → ----- ( IA – B) A min max W( I– H) b[ n],a[ n] ω M/2 min max W(ω) I( ω)e jωM/2 ⎛ ⎞ ⎜ – ∑c kcosωk⎟ ck ω ⎝ ⎠ k=0 min W( I– H) or min E subject to E( ω) < ε(ω)
Page 2 and 3:
© 2002 by CRC Press LLC
Page 6 and 7:
© 2002 by CRC Press LLC Fernanda p
Page 8 and 9:
Locating Your Topic Several avenues
Page 10 and 11:
Krste Asanovic Massachusetts Instit
Page 12 and 13:
Page 14 and 15:
Page 16 and 17:
7 8 9 Architectures for Low Power P
Page 18 and 19:
SECTION VII Communications and Netw
Page 20 and 21:
45 Testing of Synchronous Sequentia
Page 22 and 23:
Hiroshi Iwai Tokyo Institute of Tec
Page 24 and 25:
FIGURE 1.2 FIGURE 1.3 © 2002 by CR
Page 26 and 27:
1.2 Downsizing below 0.1 © 2002 by
Page 28 and 29:
FIGURE 1.9 Subthreshold leakage cur
Page 30 and 31:
FIGURE 1.13 Epitaxial channel [9].
Page 32 and 33:
gate length reduction was accelerat
Page 34 and 35:
of the prediction. Until only sever
Page 36 and 37:
FIGURE 1.22 Clarke number of elemen
Page 38 and 39:
1.5 Source and Drain Figure 1.25 sh
Page 40 and 41:
FIGURE 1.27 Retrograde profile. FIG
Page 42 and 43:
TABLE 1.6 Trend of Interconnect by
Page 44 and 45:
TABLE 1.9a Trend of DRAM Cell: Stac
Page 46 and 47:
FIGURE 1.36 Trend of gate length. F
Page 48 and 49:
References 1. D. Kahng and M. M. At
Page 50 and 51:
40. B. H. Lee, R. Choi, L. Kang, S.
Page 52 and 53:
outputs of the gate regardless of t
Page 54 and 55:
FIGURE 2.4 circuit. This is the bas
Page 56 and 57:
FIGURE 2.8 Two different realizatio
Page 58 and 59:
FIGURE 2.12 Multifunction circuitry
Page 60 and 61:
Dynamic Logic Circuits The basic id
Page 62 and 63:
transistors in the pull-down networ
Page 64 and 65:
In Fig. 2.21(d), the cross-coupled
Page 66 and 67:
FIGURE 2.23 Different configuration
Page 68 and 69:
In some literature, the authors lik
Page 70 and 71:
Concluding Remarks The feature size
Page 72 and 73:
FIGURE 2.30 Other pass-transistor c
Page 74 and 75:
FIGURE 2.34 Dual-rail, pass-transis
Page 76 and 77:
Shannon expansion, as shown below,
Page 78 and 79:
FIGURE 2.41 Logic circuit for Out =
Page 80 and 81:
FIGURE 2.45 Example decomposed BDD.
Page 82 and 83:
FIGURE 2.50 Diffusion-area sharing
Page 84 and 85:
FIGURE 2.54 Relationship between co
Page 86 and 87:
29. Shiple, T. R., Hojati, R., Sang
Page 88 and 89:
FIGURE 2.58 DTMOS devices: (a) stan
Page 90 and 91:
the design into a BDD representatio
Page 92 and 93:
FIGURE 2.63 Circuit diagram of 2-in
Page 94 and 95:
FIGURE 2.67 Synthesis of 2-input AN
Page 96 and 97:
pass-transistor logic, constrained
Page 98 and 99:
16. Bryant, R., Graph-based algorit
Page 100 and 101:
As shown in Fig. 2.79, the MOSFET d
Page 102 and 103:
n + SiO 2 FIGURE 2.80 No reverse bo
Page 104 and 105:
structures are a powerful solution
Page 106 and 107:
SiO 2 Epitaxial Si Double Layered P
Page 108 and 109:
PD-SOI Application to High-Performa
Page 110 and 111:
LO FIGURE 2.91 History effects. sta
Page 112 and 113:
weight, lower cost, a wireless inte
Page 114 and 115:
TABLE 2.7 Performance of sub-1 V MT
Page 116 and 117:
X X FIGURE 2.99 1 V A/D converter u
Page 118 and 119:
When the communication range is 10
Page 120 and 121:
13. Nakashima, S., et al., Thicknes
Page 122 and 123:
FIGURE 3.1 Conventional ECL circuit
Page 124 and 125:
FIGURE 3.4 FIGURE 3.5 IPULL-DOWN, f
Page 126 and 127:
FIGURE 3.7 V REG voltage regulator
Page 128 and 129:
FIGURE 3.10 Layout of inverter gate
Page 130 and 131:
FIGURE 3.14 Power consumption versu
Page 132 and 133:
I/O Pads, is 60 mW for the multiple
Page 134 and 135:
FIGURE 3.21 Maximum data rate vs. V
Page 136 and 137:
John C. McCallum National Universit
Page 138 and 139:
enchmark took between 15.7 and 5115
Page 140 and 141:
The improvements in line widths, ch
Page 142 and 143:
performance. Extensive lists of SPE
Page 144 and 145:
TABLE 4.6 Functions of Memory and S
Page 146 and 147:
Memory Price ($/MB) FIGURE 4.3 Cost
Page 148 and 149:
TABLE 4.8 Disk Drive Characteristic
Page 150 and 151:
4.6 Summary The performance of comp
Page 152 and 153:
53. Curnow, H. J., and Wichmann, B.
Page 154 and 155:
Computer Systems and Architecture
Page 156 and 157:
advances that have been made in dev
Page 158 and 159:
Server Types Servers are optimized
Page 160 and 161:
Total Cost of Ownership Another con
Page 162 and 163:
edundant memory-bit steering, and s
Page 164 and 165:
majority of the users. Hardware opt
Page 166 and 167:
processor implementations. In later
Page 168 and 169:
FIGURE 5.7 an operand. For larger c
Page 170 and 171:
Example 2 This example contrasts th
Page 172 and 173:
Unlike the Defoe, the IA-64 archite
Page 174 and 175:
This 3-phase approach fails to expl
Page 176 and 177:
6. Scott Rixner, William J. Dally,
Page 178 and 179:
Shared-memory vector architectures
Page 180 and 181:
The vector ISA usually fixes the ma
Page 182 and 183:
FIGURE 5.12 A vector unit construct
Page 184 and 185:
use of loops optimized for certain
Page 186 and 187:
9. Espasa, R., Advanced Vector Arch
Page 188 and 189:
thread management (including run-ti
Page 190 and 191:
In the message passing model, inter
Page 192 and 193:
multithreaded hardware, possibly by
Page 194 and 195:
synchronization) and usually contai
Page 196 and 197:
a common register space, it is impo
Page 198 and 199:
FIGURE 5.16 When a load request is
Page 200 and 201:
list a few helpful references to wh
Page 202 and 203:
38. S. Wallace, B. Calder, and D. T
Page 204 and 205:
Of course, SIMD machines have limit
Page 206 and 207:
computation, it will decrease execu
Page 208 and 209:
FIGURE 5.19 An 8 × 8 baseline netw
Page 210 and 211:
Since then, we have seen constant e
Page 212 and 213:
Stack: Data: Text: Virtual Space FI
Page 214 and 215:
FIGURE 5.25 Shared memory. Shared m
Page 216 and 217:
0 2 GB Text Init. Data Bss Heap . .
Page 218 and 219:
In general, if the necessary transl
Page 220 and 221:
Mark Smotherman Clemson University
Page 222 and 223:
Studies of Instruction-Level Parall
Page 224 and 225:
Modern Designs Most high-performanc
Page 226 and 227:
The principle of register renaming
Page 228 and 229:
FIGURE 6.2 issued into the RS, (ii)
Page 230 and 231:
Issue Dispatch FIGURE 6.4 The proce
Page 232 and 233:
FIGURE 6.6 Scope of register renami
Page 234 and 235:
FIGURE 6.9 State transition diagram
Page 236 and 237:
Thus, the maximal number of instruc
Page 238 and 239:
In addition, if rename buffers are
Page 240 and 241:
it, whose role will be explained su
Page 242 and 243:
As Fig. 6.13 shows, the latest proc
Page 244 and 245:
for recovery. Both processors incor
Page 246 and 247:
FIGURE C. The principle of direct i
Page 248 and 249:
13. White, S. and Reysa, J., PowerP
Page 250 and 251:
FIGURE 6.14 A branch flowing throug
Page 252 and 253:
is that mispredictions limit the pr
Page 254 and 255:
fetch engine to identify which inst
Page 256 and 257:
FIGURE 6.17 A schematic for a bimod
Page 258 and 259:
FIGURE 6.20 A schematic for a GAg g
Page 260 and 261:
FIGURE 6.22 A schematic for a hybri
Page 262 and 263:
time this branch is seen, those bit
Page 264 and 265:
FIGURE 6.23 Branch prediction accur
Page 266 and 267:
11. Price, C., MIPS IV Instruction
Page 268 and 269:
transporting digital bits, whereas
Page 270 and 271:
FIGURE 6.25 The system architecture
Page 272 and 273:
Finally, because the main task of n
Page 274 and 275:
Pradip Bose IBM T. J. Watson Resear
Page 276 and 277:
frequency © 2002 by CRC Press LLC
Page 278 and 279:
The “mips” metric for performan
Page 280 and 281:
Hence, in this paper, we do not dwe
Page 282 and 283:
FIGURE 7.4 Parallel SIMD architectu
Page 284 and 285:
dynamic prediction of such idle mod
Page 286 and 287:
FIGURE 7.7 High-level block-diagram
Page 288 and 289:
(measured as a performance over pow
Page 290 and 291:
Steady-state BIPS FIGURE 7.9 Perfor
Page 292 and 293:
8. Larson, A. G., “Cost-effective
Page 294 and 295:
Jozo J. Dujmović San Francisco Sta
Page 296 and 297:
x FIGURE 8.1 Movement of the disk I
Page 298 and 299:
The critical distance x ∗ is Ther
Page 300 and 301:
Hence, the average seek time for th
Page 302 and 303:
FIGURE 8.4 Four-parameter exponenti
Page 304 and 305:
Access Time [ms] 2 0 0 FIGURE 8.6 M
Page 306 and 307:
TABLE 8.1 Classification of Eight B
Page 308 and 309:
The traditional load independent me
Page 310 and 311:
Response Time [seconds] 290 270 250
Page 312 and 313:
FIGURE 8.14 Prediction errors e(p)
Page 314 and 315:
8.2 Performance Evaluation: Techniq
Page 316 and 317:
is generally the most important mea
Page 318 and 319:
tool to profile programs on the Alp
Page 320 and 321:
driven simulation has two major pro
Page 322 and 323:
A variety of profiling tools exist
Page 324 and 325:
SPLASH, the SPLASH suite was create
Page 326 and 327:
different types and complexity eith
Page 328 and 329:
Table 8.8 provides sources for the
Page 330 and 331:
37. MediaBench benchmarks, http://w
Page 332 and 333:
(a) Instruction Cache (b) Trace Cac
Page 334 and 335:
PE 0 Local Register File local bypa
Page 336 and 337:
The large trace processor instructi
Page 338 and 339:
11. S. Melvin, M. Shebanow, and Y.
Page 340 and 341:
complement numbers. Sign magnitude
Page 342 and 343:
where ak, bk, and ck are the inputs
Page 344 and 345:
k + 1, etc. Extending to a third st
Page 346 and 347:
a 12:15 b 12:15 4-Bit RCA s 12:15 F
Page 348 and 349:
FIGURE 9.8 Two’s complement subtr
Page 350 and 351:
FIGURE 9.10 Unsigned 6 by 6 array m
Page 352 and 353:
Digit Recurrent Division The most c
Page 354 and 355:
FIGURE 9.14 Nonrestoring division.
Page 356 and 357:
The Newton-Raphson division algorit
Page 358 and 359:
FIGURE 9.18 Floating-point addition
Page 360 and 361:
9.2 Fast Adders and Multipliers Gen
Page 362 and 363:
FIGURE 9.20 Half-adder circuit. is
Page 364 and 365:
gi pi FIGURE 9.22(b) Carry skip cir
Page 366 and 367:
Assuming that a single level of the
Page 368 and 369:
Array-Type Multiplier The simplest
Page 370 and 371:
p1i,j p2i,j p3i,j p4i,j FIGURE 9.27
Page 372 and 373:
The partial product PP j is to be c
Page 374 and 375:
The sum SGN of the whole extended b
Page 376 and 377:
FIGURE 9.31 54 × 54-bit parallel m
Page 378 and 379:
6. Svensson, C. and Tjarnstrom, R.,
Page 380 and 381:
Design Techniques III 10 Timing and
Page 382 and 383:
FIGURE 10.1 Typical chip interface.
Page 384 and 385:
Loop Components PLLs and DLLs share
Page 386 and 387:
delay is some fraction of the input
Page 388 and 389:
esults from the voltage across the
Page 390 and 391:
© 2002 by CRC Press LLC TABLE 10.2
Page 392 and 393:
db(H( ω)) FIGURE 10.6 PLL closed-l
Page 394 and 395:
ω )/G O) db(T(ω ph(T( )/π) FIGUR
Page 396 and 397:
Phase Margin (deg) FIGURE 10.10 PLL
Page 398 and 399:
FIGURE 10.11 Measured PLL jitter hi
Page 400 and 401:
FIGURE 10.13 DLL output jitter sens
Page 402 and 403:
FIGURE 10.18 PLL output jitter sens
Page 404 and 405:
Active supply filters employ amplif
Page 406 and 407:
FIGURE 10.19 Single-ended delay ele
Page 408 and 409:
Frequency (GHz) FIGURE 10.23 Freque
Page 410 and 411:
FIGURE 10.25 Push-pull charge pump.
Page 412 and 413:
Circuit Summary In general, all DLL
Page 414 and 415:
5. T. Lee, et al., “A 2.5V CMOS D
Page 416 and 417:
introduced in [3], is used to repre
Page 418 and 419:
FIGURE 10.31 Setup and hold time ti
Page 420 and 421:
FIGURE 10.34 Max-timing diagrams fo
Page 422 and 423:
FIGURE 10.37 Time borrowing for sin
Page 424 and 425:
FIGURE 10.39 Max-timing for single-
Page 426 and 427:
Min-Timing In contrast to max-timin
Page 428 and 429:
FIGURE 10.46 Min-timing diagrams fo
Page 430 and 431:
FIGURE 10.49 Edge-triggered, flip-f
Page 432 and 433:
FIGURE 10.51 FIGURE 10.52 Max-timin
Page 434 and 435:
FIGURE 10.53 Transparent-high latch
Page 436 and 437:
FIGURE 10.57 Complementary TSPC tra
Page 438 and 439:
FIGURE 10.61 A positive, edge-trigg
Page 440 and 441:
FIGURE 10.66 Pulsed latches. FIGURE
Page 442 and 443:
assigned, based on the subcircuit t
Page 444 and 445:
FIGURE 10.71 Scan chain for dual-ph
Page 446 and 447:
and SEB, which are complementary, c
Page 448 and 449:
when used as a flip-flop, the NAND3
Page 450 and 451:
FIGURE 10.75 Integrated memory for
Page 452 and 453:
Memory Cell Bit# Bit FIGURE 10.78 A
Page 454 and 455:
FIGURE 10.80 Modeling process varia
Page 456 and 457:
FIGURE 10.83 A column circuit. FIGU
Page 458 and 459:
advantage of this circuit, compared
Page 460 and 461:
K. Wayne Current University of Cali
Page 462 and 463:
11.2 Nonvolatile Multiple-Valued Me
Page 464 and 465:
Multiple-Valued EEPROM and Flash Me
Page 466 and 467:
direct properly scaled and logicall
Page 468 and 469:
Current comparators are a critical
Page 470 and 471:
FIGURE 11.4 Current-mode CMOS quate
Page 472 and 473:
FIGURE 11.6 Current-mode CMOS quate
Page 474 and 475:
observed with these circuits are ab
Page 476 and 477:
FIGURE 11.11 Current-mode CMOS quat
Page 478 and 479:
FIGURE 11.12 Current-mode CMOS latc
Page 480 and 481:
FIGURE 11.14 Current-mode CMOS anal
Page 482 and 483:
esults confirm the DC transfer func
Page 484 and 485:
19. T. T. Dao, “Threshold I2L and
Page 486 and 487:
FIGURE 12.1 Device technologies use
Page 488 and 489:
selected depending on the number of
Page 490 and 491:
Architecture of Newer Generation FP
Page 492 and 493:
FIGURE 12.6 An example of a simple
Page 494 and 495:
tools, the + 1 operation is a speci
Page 496 and 497:
download the programming data to th
Page 498 and 499:
FIGURE 13.1 High-performance microp
Page 500 and 501:
FIGURE 13.4 TABLE 13.1 combinationa
Page 502 and 503:
accurate wire modelling while limit
Page 504 and 505:
FIGURE 13.6 Dual-rail, multiple-out
Page 506 and 507:
FIGURE 13.10 Effect of output inver
Page 508 and 509:
FIGURE 13.11 Unfooted dynamic 4:1 m
Page 510 and 511:
(4) the limit of designers to manag
Page 512 and 513:
© 2002 by CRC Press LLC IV Design
Page 514 and 515:
FIGURE 14.1 FIGURE 14.2 newer semic
Page 516 and 517:
The cost impact of power consumptio
Page 518 and 519:
In any case, the move toward “Gre
Page 520 and 521:
This static current is obviously un
Page 522 and 523:
14.2 Power Estimation As we saw in
Page 524 and 525:
lock as a function of various param
Page 526 and 527:
FIGURE 14.8 Sleep transistors to co
Page 528 and 529:
FIGURE 14.12 Data enabling. In addi
Page 530 and 531:
Power Reduction through CAD Tools P
Page 532 and 533:
AMPS AMPS is a circuit power optimi
Page 534 and 535:
Masayuki Miyazaki Hitachi, Ltd. 15.
Page 536 and 537:
15.3 Supply Voltage Management Supp
Page 538 and 539:
FIGURE 15.4 MT-CMOS balloon circuit
Page 540 and 541:
FIGURE 15.9 EVT-CMOS circuit design
Page 542 and 543:
FIGURE 15.12 VT-CMOS block diagram
Page 544 and 545:
FIGURE 15.15 SA-V t CMOS scheme wit
Page 546 and 547:
FIGURE 15.17 Floating-point datapat
Page 548 and 549:
Vivek De Intel Corporation Ali Kesh
Page 550 and 551:
FIGURE 16.3 n-channel ID vs. VG sho
Page 552 and 553:
Gate-Induced Drain Leakage (I 4) GI
Page 554 and 555:
FIGURE 16.7 Two-nMOS stack in a two
Page 556 and 557:
FIGURE 16.11 Four-input NAND NMOS s
Page 558 and 559:
FIGURE 16.12 Distribution of standb
Page 560 and 561:
Die count FIGURE 16.16 (a) Adaptive
Page 562 and 563:
due to adaptive body bias worsens w
Page 564 and 565:
Thomas D. Burd University of Califo
Page 566 and 567:
the parameter to be maximized since
Page 568 and 569:
17.3 Dynamically Varying Voltage If
Page 570 and 571:
The voltage converter required for
Page 572 and 573:
FIGURE 17.7 DVS improvement for UI
Page 574 and 575:
FIGURE 17.10 Measured throughput vs
Page 576 and 577:
FIGURE 17.12 Sources of noise margi
Page 578 and 579:
FIGURE 17.15 Ring oscillator adapti
Page 580 and 581:
FIGURE 17.17 Sense-amp delay variat
Page 582 and 583:
Christian Piguet CSEM: Centre Suiss
Page 584 and 585:
Some Basic Rules There are some bas
Page 586 and 587:
TABLE 18.2 Looped 8-bit Multiply Pr
Page 588 and 589:
FIGURE 18.4 new architecture paradi
Page 590 and 591:
FIGURE 18.6 FIGURE 18.7 the second
Page 592 and 593:
FIGURE 18.9 FIGURE 18.10 With latch
Page 594 and 595:
18.6 Low-Power Memories As memories
Page 596 and 597:
connected to the main bitline (only
Page 598 and 599:
is today only about a factor of 2 d
Page 600 and 601:
Katsunori Seno SONY Corporation 19.
Page 602 and 603:
FIGURE 19.2 FIGURE 19.3 This is a c
Page 604 and 605:
FIGURE 19.6 FIGURE 19.7 FPGA sacrif
Page 606 and 607:
FIGURE 19.9 RAWn precharge FIGURE 1
Page 608 and 609:
a fixed given standard. References
Page 610 and 611:
Hendrawan Soeleman Purdue Universit
Page 612 and 613:
for a short period of time when bot
Page 614 and 615:
Total Average Power Putting togethe
Page 616 and 617:
Signal Probability Calculation In c
Page 618 and 619:
Example Given y = x 1 + x 2. Find P
Page 620 and 621:
A B F FIGURE 20.7 Unfactorized and
Page 622 and 623:
etween successive transitions is a
Page 624 and 625:
FIGURE 20.9 A logic gate and its co
Page 626 and 627:
Results Using Probabilistic Techniq
Page 628 and 629:
FIGURE 20.12 Probabilistic and stat
Page 630 and 631:
14. VLSI Microprocessors: A Guide t
Page 632 and 633:
0 V to a voltage V in time T throug
Page 634 and 635:
a small fraction of circuit nodes t
Page 636 and 637:
FIGURE 21.6 (a) E-R latch, (b) timi
Page 638 and 639:
FIGURE 21.8 Potential E-R latch for
Page 640 and 641:
The only difference between the two
Page 642 and 643:
FIGURE 21.14 (a) Clock-powered stat
Page 644 and 645:
FIGURE 21.17 The three drivers used
Page 646 and 647:
FIGURE 21.20 Energy-delay product (
Page 648 and 649:
FIGURE 21.22 AC-1 clock-driver sche
Page 650 and 651:
clock-powered nodes accounted for 8
Page 652 and 653:
Two generations of clock-powered mi
Page 654 and 655:
29. Athas, W. C., Tzartzanis, N., M
Page 656 and 657:
Wayne Wolf Princeton University 22.
Page 658 and 659:
so a CPU could be built in reconfig
Page 660 and 661:
optimized processes. Although embed
Page 662 and 663:
FIGURE 22.4 they are most useful wh
Page 664 and 665:
• How should processes be allocat
Page 666 and 667:
25 memory system activity. If the c
Page 668 and 669:
Jonathan W. Valvano University of T
Page 670 and 671: FIGURE 23.2 6808, I/O ports A and B
Page 672 and 673: personnel so that they are proficie
Page 674 and 675: BDM can provide the ability to obse
Page 676 and 677: minor modifications to the finite s
Page 678 and 679: Many components are included in a d
Page 680 and 681: will saturate resulting in a bang-b
Page 682 and 683: Two approaches are used to synchron
Page 684 and 685: Fred J. Taylor University of Florid
Page 686 and 687: The output of a linear system havin
Page 688 and 689: FIGURE 24.2 Effects of windowing an
Page 690 and 691: frequency range ±f Nyquist = ±f s
Page 692 and 693: performance, complexity, and precis
Page 694 and 695: overflows of intermediate sums. Tha
Page 696 and 697: 24.7 Applications “DSP” has bec
Page 698 and 699: DSP (Digital Signal Processor) or D
Page 700 and 701: PC as a Terminal (Modem) The PC is
Page 702 and 703: characteristics: • Fixed pictures
Page 704 and 705: HDTV (and Digital Television) If th
Page 706 and 707: Modem Banks This is the first of th
Page 708 and 709: 25.7 Automotive, Industrial Althoug
Page 710 and 711: 36. MITEL Semiconductor: www.semico
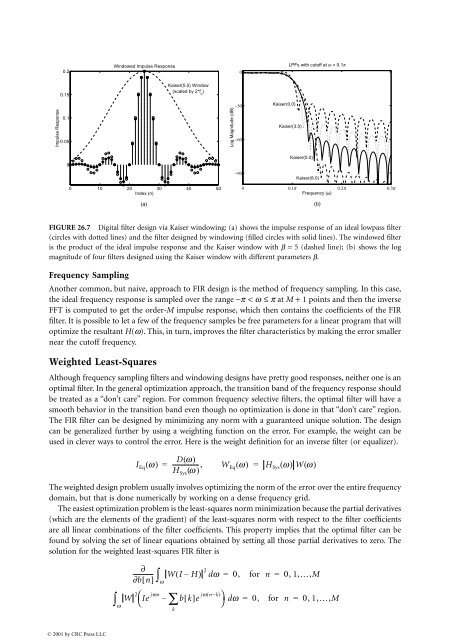
Page 712 and 713: 26.2 Digital Filters The theory of
Page 714 and 715: |H | 1 FIGURE 26.1 Frequency select
Page 716 and 717: TABLE 26.1 Filter Design Comparison
Page 718 and 719: frequency response involves some al
Page 722 and 723: This constrained magnitude problem
Page 724 and 725: FIGURE 26.8 Block diagram of the ge
Page 726 and 727: 11. Ikehara, M., Tanaka, H., and Ku
Page 728 and 729: Adam Dabrowski Poznan University To
Page 730 and 731: −12 2 The reference in this case
Page 732 and 733: FIGURE 27.1 Two-band filter bank: (
Page 734 and 735: FIGURE 27.5 Critical bandwidth and
Page 736 and 737: FIGURE 27.7 Threshold of audibility
Page 738 and 739: FIGURE 27.10 Critical band index in
Page 740 and 741: FIGURE 27.13 Simplified model of th
Page 742 and 743: All described masking effects are e
Page 744 and 745: where From Eqs. (27.32) and (27.33)
Page 746 and 747: eal-time. Although floating-point p
Page 748 and 749: FIGURE 27.19 Overlapped, power comp
Page 750 and 751: FIGURE 27.21 Symmetrical FIR filter
Page 752 and 753: In the MPEG-1 encoder an efficient
Page 754 and 755: These first two approaches can be m
Page 756 and 757: FIGURE 27.27 ADPCM: (a) encoder, (b
Page 758 and 759: FIGURE 27.30 General scheme of the
Page 760 and 761: A new standard MPEG-7, named the mu
Page 762 and 763: FIGURE 27.32 AC-3 encoder. FIGURE 2
Page 764 and 765: 29. Marven, C. and Ewers, G., A sim
Page 766 and 767: FIGURE 28.1 FIGURE 28.2 of the huma
Page 768 and 769: FIGURE 28.5 image of reasonable qua
Page 770 and 771:
Consider the case of a simple 2-D
Page 772 and 773:
FIGURE 28.8 A sampled spatiotempora
Page 774 and 775:
oth high spatial frequency componen
Page 776 and 777:
If it were separable (that is, H(ξ
Page 778 and 779:
The first hypothesis (the less plau
Page 780 and 781:
FIGURE 28.17 The real (top) and ima
Page 782 and 783:
FIGURE 28.18 The resolution of a ti
Page 784 and 785:
FIGURE 28.20 Motion estimation by b
Page 786 and 787:
where the superscripts n and n + 1
Page 788 and 789:
must be found via a finite set of o
Page 790 and 791:
The methods in this subsection are
Page 792 and 793:
FIGURE 28.28 The split phase. Using
Page 794 and 795:
35. Y.-T. Wu, T. Kanade, J. Cohn, a
Page 796 and 797:
29.2 Power Dissipation in Digital C
Page 798 and 799:
additional power benefits. Efficien
Page 800 and 801:
Power savings are higher than simpl
Page 802 and 803:
A priori knowledge of data stream d
Page 804 and 805:
FIGURE 29.7 DCT Chip [my DCT] avera
Page 806 and 807:
19. S. Uramoto et al. A 100 MHz 2-D
Page 808 and 809:
Anna Hać University of Hawaii 30.1
Page 810 and 811:
Using TCP/IP also makes the network
Page 812 and 813:
this is for one mobile host which i
Page 814 and 815:
TDMA Time-division multiple access
Page 816 and 817:
path delay. The two measures of the
Page 818 and 819:
are under the control of the system
Page 820 and 821:
the bandwidth reserved in the targe
Page 822 and 823:
Chik-Kong Ken Yang University of Ca
Page 824 and 825:
FIGURE 31.3 attenuation (dB) -3.0 -
Page 826 and 827:
FIGURE 31.5 to handle large voltage
Page 828 and 829:
p_o V bias FIGURE 31.8 High-impedan
Page 830 and 831:
out[n] a0 FIGURE 31.11 Transmitter
Page 832 and 833:
FIGURE 31.15 Receiver design using
Page 834 and 835:
digitally by first feeding the inpu
Page 836 and 837:
FIGURE 31.19 90 o locking using XOR
Page 838 and 839:
Power of these links is becoming an
Page 840 and 841:
46. Takahashi, T. et al., “A CMOS
Page 842 and 843:
Many computer programs exhibit some
Page 844 and 845:
32.3 Related Memory Models, Hierarc
Page 846 and 847:
32.6 External Sorting and Related P
Page 848 and 849:
uns, each striped across the disks.
Page 850 and 851:
Matrix transposition is the special
Page 852 and 853:
of satellite images is over one ter
Page 854 and 855:
TABLE 32.3 Best Known I/O Bounds fo
Page 856 and 857:
e accessed directly in a single I/O
Page 858 and 859:
implementations of priority queues
Page 860 and 861:
By the reduction in [52], a data st
Page 862 and 863:
set of experiments on various text
Page 864 and 865:
3. A. Acharya, M. Uysal, and J. Sal
Page 866 and 867:
44. J. L. Bentley and J. B. Saxe. D
Page 868 and 869:
85. P. Ferragina and F. Luccio. Dyn
Page 870 and 871:
128. V. Kumar and E. Schwabe. Impro
Page 872 and 873:
173. H. Samet. The Design and Analy
Page 874 and 875:
Peter J. Varman Rice University 33.
Page 876 and 877:
need for fast transfers, up to 1 Gb
Page 878 and 879:
In contrast to prefetching that mas
Page 880 and 881:
The ERF algorithm was analyzed in [
Page 882 and 883:
increment lowestPriorityOnDisk(disk
Page 884 and 885:
External or out-of-core algorithms
Page 886 and 887:
33. M. Kallahalla and P. J. Varman.
Page 888 and 889:
advanced, reaching the point where
Page 890 and 891:
FIGURE 34.3 FIGURE 34.4 defines the
Page 892 and 893:
FIGURE 34.5 Trellis representation
Page 894 and 895:
FIGURE 34.7 Data and servo sectors.
Page 896 and 897:
References 1. S. H. Charrap, P. L.
Page 898 and 899:
High-frequency noise is then remove
Page 900 and 901:
The various components of (34.3) ar
Page 902 and 903:
sequences are more complex, and occ
Page 904 and 905:
ange of 10 −12 -10 −15 . Anothe
Page 906 and 907:
strategies are reviewed, which have
Page 908 and 909:
FIGURE 34.13 Magnitude response for
Page 910 and 911:
taps as an approximation of the Typ
Page 912 and 913:
FIGURE 34.18 CTF BER performance de
Page 914 and 915:
TABLE 34.1 Examples of Equalizers I
Page 916 and 917:
(i) Symbol rate VCO based timing re
Page 918 and 919:
Symbol Rate Timing Recovery Schemes
Page 920 and 921:
where B = B 1 + B 2 + 1 is the size
Page 922 and 923:
in � out � d(k) FIGURE 34.26 Ti
Page 924 and 925:
�(k) z -L FIGURE 34.27 Linearized
Page 926 and 927:
10 −4 and 10 −2 . The steady-st
Page 928 and 929:
16. J. Sonntag, et al., “A high s
Page 930 and 931:
y a special sequence known as the a
Page 932 and 933:
FIGURE 34.36 An example of two Gray
Page 934 and 935:
track n track n +1 FIGURE 34.38 The
Page 936 and 937:
FIGURE 34.40 The phase format. Posi
Page 938 and 939:
increase linear density while mitig
Page 940 and 941:
FIGURE 34.43 Two equivalent constra
Page 942 and 943:
FIGURE 34.44 Possible pairs of sequ
Page 944 and 945:
Distance δ min,C can be bounded as
Page 946 and 947:
FIGURE 34.45 Standard concatenation
Page 948 and 949:
30. E. Soljanin, “On-track and of
Page 950 and 951:
The next block is PRE. What is PR?
Page 952 and 953:
In the above example, we see that s
Page 954 and 955:
FIGURE 34.52 Feedback detector. Cat
Page 956 and 957:
FIGURE 34.54 Decision feedback equa
Page 958 and 959:
esponse (this is also valid for dif
Page 960 and 961:
its use, while the computational, o
Page 962 and 963:
FIGURE 34.58 Viterbi algorithm dete
Page 964 and 965:
Noise-Predictive Maximum Likelihood
Page 966 and 967:
The error event likelihoods are cal
Page 968 and 969:
Metric-First Algorithms Metric-firs
Page 970 and 971:
termination at the same time. Howev
Page 972 and 973:
13. J. Hagenauer, “Applications o
Page 974 and 975:
Given a code C of length n and dime
Page 976 and 977:
Notice that, although a code may ha
Page 978 and 979:
Not many perfect codes exist. In th
Page 980 and 981:
Theorem 1 (Shannon) For any � > 0
Page 982 and 983:
If we write the codewords as polyno
Page 984 and 985:
Let © 2002 by CRC Press LLC 1 1 K
Page 986 and 987:
which, in polynomial form, is Let E
Page 988 and 989:
m Σl=0 because a l = (a m+1 − 1)
Page 990 and 991:
Evaluating the syndromes, we obtain
Page 992 and 993:
FIGURE 34.63 Interleaving m times o
Page 994 and 995:
Operating System © 2002 by CRC Pre
Page 996 and 997:
systems, the most notable example b
Page 998 and 999:
35.3 Components of Distributed Oper
Page 1000 and 1001:
Message-passing IPC shares many cha
Page 1002 and 1003:
process at any arbitrary stage in i
Page 1004 and 1005:
Few attempts were made in the past
Page 1006 and 1007:
alternate years with SOSP), and the
Page 1008 and 1009:
© 2002 by CRC Press LLC 42 Mobile
Page 1010 and 1011:
FIGURE 36.1 were introduced; howeve
Page 1012 and 1013:
FPGAs by providing on-chip memory f
Page 1014 and 1015:
FIGURE 36.3 There is a considerable
Page 1016 and 1017:
FIGURE 36.4 The general form of the
Page 1018 and 1019:
FIGURE 36.6 If a VPB can cover all
Page 1020 and 1021:
John Morris University of Western A
Page 1022 and 1023:
FIGURE 37.1 Simplified block diagra
Page 1024 and 1025:
inverters, and the programmable mul
Page 1026 and 1027:
Programmable Active Memories (PAM)
Page 1028 and 1029:
measured in megabits, not megabytes
Page 1030 and 1031:
from modern FPGAs, e.g., Altera’s
Page 1032 and 1033:
Regularity A processing pipeline wi
Page 1034 and 1035:
Other Languages Other routes from h
Page 1036 and 1037:
29. Bergmann, N.W., and Dawood, A.,
Page 1038 and 1039:
FIGURE 37.8 Basic architectures for
Page 1040 and 1041:
Selected Applications Several class
Page 1042 and 1043:
Development Systems Developing appl
Page 1044 and 1045:
implementation. Reconfigurable or r
Page 1046 and 1047:
The designer starts the generation
Page 1048 and 1049:
lock but allows multiple instructio
Page 1050 and 1051:
data-types that are mapped to TIE r
Page 1052 and 1053:
Conclusions Configurable and extens
Page 1054 and 1055:
FIGURE 38.1 Average vehicle speed.
Page 1056 and 1057:
AHS means advanced cruise-assist hi
Page 1058 and 1059:
TABLE 38.3 navigation systems VICS
Page 1060 and 1061:
FIGURE 38.9 FIGURE 38.10 a map data
Page 1062 and 1063:
FIGURE 38.13 The four basic functio
Page 1064 and 1065:
Support of Safe Driving System The
Page 1066 and 1067:
System evaluation, the fourth issue
Page 1068 and 1069:
FIGURE 38.18 Summarizing the three
Page 1070 and 1071:
uilder tools serving to build MMI o
Page 1072 and 1073:
FIGURE 38.23 FIGURE 38.24 automaker
Page 1074 and 1075:
FIGURE 38.26 FIGURE 38.27 The first
Page 1076 and 1077:
FIGURE 38.30 FIGURE 38.31 a kind of
Page 1078 and 1079:
To Probe Further In this field, the
Page 1080 and 1081:
FIGURE 39.1 of more versatile media
Page 1082 and 1083:
1 • 3DNow! 1 [11,12] from AMD,
Page 1084 and 1085:
FIGURE 39.6 In the packed add instr
Page 1086 and 1087:
If saturation arithmetic is used in
Page 1088 and 1089:
TABLE 39.1 Examples of Operations T
Page 1090 and 1091:
FIGURE 39.10 PAVG R c, R a, R b: Pa
Page 1092 and 1093:
FIGURE 39.13 Packed compare instruc
Page 1094 and 1095:
FIGURE 39.17 Packed multiply high i
Page 1096 and 1097:
FIGURE 39.20 Packed multiply left i
Page 1098 and 1099:
FIGURE 39.23 In the packed multiply
Page 1100 and 1101:
TABLE 39.4 Packed Integer Multiplic
Page 1102 and 1103:
Subword Permutation Instructions In
Page 1104 and 1105:
is n log 2(n). Table 39.6 shows how
Page 1106 and 1107:
FIGURE 39.33 Mix left instruction.
Page 1108 and 1109:
TABLE 39.7 Subword Permutation Inst
Page 1110 and 1111:
TABLE 39.9 IA-64 uses FPMA and FPMS
Page 1112 and 1113:
The two-bit result field is written
Page 1114 and 1115:
source register. These three FP mix
Page 1116 and 1117:
13. Motorola, “AltiVec technology
Page 1118 and 1119:
FIGURE 39.48 ManArray 1 × 2 core e
Page 1120 and 1121:
FIGURE 39.50 Hypercube interconnect
Page 1122 and 1123:
FIGURE 39.53 Host DSP software laye
Page 1124 and 1125:
Benchmark Data Type Performance 256
Page 1126 and 1127:
FIGURE 39.56 Simplified schematic o
Page 1128 and 1129:
Gaming applications often require a
Page 1130 and 1131:
system, and the application program
Page 1132 and 1133:
FIGURE 39.60 FIGURE 39.61 FIGURE 39
Page 1134 and 1135:
FIGURE 39.64 shifting place limits
Page 1136 and 1137:
FIGURE 39.66 pitch Address Looping
Page 1138 and 1139:
FIGURE 39.69 gain of the filter. It
Page 1140 and 1141:
as a core to integrate onto the sam
Page 1142 and 1143:
7. Rossum, D., Constraint based aud
Page 1144 and 1145:
FIGURE 39.74 Procedure for simulate
Page 1146 and 1147:
The fitness value of an individual
Page 1148 and 1149:
FIGURE 39.77 The tabu list can be v
Page 1150 and 1151:
Intermediate-term memory component
Page 1152 and 1153:
FIGURE 39.81 Selection. FIGURE 39.8
Page 1154 and 1155:
Work on parallelization of the tabu
Page 1156 and 1157:
Acknowledgment The authors acknowle
Page 1158 and 1159:
47. L. K. Grover. A new Simulated A
Page 1160 and 1161:
93. E. M. Rudnick, J. H. Patel, G.
Page 1162 and 1163:
138. Youn-Long Lin, Yu-Chin Hsu, an
Page 1164 and 1165:
This architecture allowed for large
Page 1166 and 1167:
FIGURE 40.3 40.3 Application Server
Page 1168 and 1169:
FIGURE 40.5 applications. CORBA cur
Page 1170 and 1171:
FIGURE 40.8 The application server
Page 1172 and 1173:
FIGURE 40.10 The proposed architect
Page 1174 and 1175:
cost at the front end. The ideal ap
Page 1176 and 1177:
FIGURE 40.12 Client-server and netw
Page 1178 and 1179:
Yoshiaki Hagiwara Sony Corporation
Page 1180 and 1181:
FIGURE 41.2 This corresponds to the
Page 1182 and 1183:
FIGURE 41.5 Buried channel CCD stru
Page 1184 and 1185:
FIGURE 41.8 Applications of CCD and
Page 1186 and 1187:
sensor (1100 K pixel) Microphone ×
Page 1188 and 1189:
�� FIGURE 41.14 Form com
Page 1190 and 1191:
FIGURE 41.16 Stack technology. Link
Page 1192 and 1193:
1st EmDRAM Product FIGURE 41.19 Emb
Page 1194 and 1195:
FIGURE 41.23 Em-DRAM process techno
Page 1196 and 1197:
John F. Alexander University of Nor
Page 1198 and 1199:
Several reasons exist for mentionin
Page 1200 and 1201:
sort of local area network. Support
Page 1202 and 1203:
Technological hurdles must be overc
Page 1204 and 1205:
FIGURE 42.1 Block diagram of (a) ge
Page 1206 and 1207:
FIGURE 42.3 Alternative FIR filter
Page 1208 and 1209:
FIGURE 42.5 Polyphase filter struct
Page 1210 and 1211:
3. E. Dahlman, Bjorn Gudmundson, M.
Page 1212 and 1213:
TABLE 42.1 Categorizing Reusable Co
Page 1214 and 1215:
FIGURE 42.11 Internet growth. FIGUR
Page 1216 and 1217:
FIGURE 42.13 Software for VoIP SoC.
Page 1218 and 1219:
FIGURE 42.17 Bandwidth trends. FIGU
Page 1220 and 1221:
The interconnections between the va
Page 1222 and 1223:
FIGURE 42.21 A typical communicatio
Page 1224 and 1225:
carry information over longer dista
Page 1226 and 1227:
however, it is not uncommon that so
Page 1228 and 1229:
node, to which the user is connecte
Page 1230 and 1231:
its information. Intuitively, this
Page 1232 and 1233:
This issue is referred to as latenc
Page 1234 and 1235:
Evolution of Standard Image/Video C
Page 1236 and 1237:
FIGURE 42.26 Sequence of zigzag-cod
Page 1238 and 1239:
FIGURE 42.29 150th Frame of origina
Page 1240 and 1241:
FIGURE 42.31 Data partitioning for
Page 1242 and 1243:
for transmitting a predictively cod
Page 1244 and 1245:
42.6 Pen-Based User Interfaces—An
Page 1246 and 1247:
FIGURE 42.35 The handwriting recogn
Page 1248 and 1249:
• No toggling between edit/contro
Page 1250 and 1251:
FIGURE 42.39 Boxplots of time to en
Page 1252 and 1253:
0 … 9 ( ) -
Page 1254 and 1255:
is using the SMIL generic media ref
Page 1256 and 1257:
FIGURE 42.47 Example of pen-and-pap
Page 1258 and 1259:
slots specifying pieces of informat
Page 1260 and 1261:
most stringent demands for low-powe
Page 1262 and 1263:
FIGURE 42.51 MIPS requirement of se
Page 1264 and 1265:
FIGURE 42.54 von Neumann architectu
Page 1266 and 1267:
FIGURE 42.57 Dual Mac architecture
Page 1268 and 1269:
FIGURE 42.59 Two data path variatio
Page 1270 and 1271:
FIGURE 42.60 Basic pipeline archite
Page 1272 and 1273:
References 1. Bahl L., Cocke J., Je
Page 1274 and 1275:
Random Oracle Model One direction o
Page 1276 and 1277:
at the end of its usefulness. A new
Page 1278 and 1279:
function and verification function
Page 1280 and 1281:
underlies the Diffie-Hellman key ag
Page 1282 and 1283:
31. Dolev, D., Dwork, C., and Naor,
Page 1284 and 1285:
R. Chandramouli Synopsys Inc. 44.1
Page 1286 and 1287:
many deficiencies in the design may
Page 1288 and 1289:
impact the performance and test ove
Page 1290 and 1291:
FIGURE 44.4 FIGURE 44.5 It becomes
Page 1292 and 1293:
SoC methodologies require synchroni
Page 1294 and 1295:
This method, however, lacks the app
Page 1296 and 1297:
FIGURE 45.2 Input formats of MILEF
Page 1298 and 1299:
FIGURE 45.3 FIGURE 45.4 Robustness
Page 1300 and 1301:
FIGURE 45.5 In Fig. 45.5 a simple e
Page 1302 and 1303:
difficult to identify for overcurre
Page 1304 and 1305:
General Approach in Comparison with
Page 1306 and 1307:
FIGURE 45.10 phase—the propagatio
Page 1308 and 1309:
shorter test sequence could possibl
Page 1310 and 1311:
Looking at results of Table 45.6, i
Page 1312 and 1313:
45.4 Summary Automatic test pattern
Page 1314 and 1315:
41. F. Brglez, H. Fujiwara: A neutr
Page 1316 and 1317:
FIGURE 46.1 Rule of ten in testing
Page 1318 and 1319:
FIGURE 46.5 FIGURE 46.6 of the DUT.
Page 1320 and 1321:
FIGURE 46.7 generate tests for ever
Page 1322 and 1323:
FIGURE 46.9 FIGURE 46.10 behavioral
Page 1324 and 1325:
Z. Stamenković University of N. St
Page 1326 and 1327:
FIGURE 47.2 Murphy’s Model The mo
Page 1328 and 1329:
where k is the total number of crit
Page 1330 and 1331:
FIGURE 47.5 Definition of IC critic
Page 1332 and 1333:
distribution [34,35]: © 2002 by CR
Page 1334 and 1335:
and, in the case of w = X 2 − X 1
Page 1336 and 1337:
Algorithm • Input: a singly linke
Page 1338 and 1339:
TRACIF takes a CIF file as input an
Page 1340 and 1341:
TABLE 47.2 Critical Area Extraction
Page 1342 and 1343:
Also, the critical areas for lithog
Page 1344 and 1345:
(enhancement of the process cleanli
Page 1346 and 1347:
28. Corsi, F. and Martino, S., Defe
show all

U. Glaeser

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?