- Page 1 and 2: FÍSICA GENERAL MUESTRA PARA EXAMEN
- Page 3 and 4: 10 CONTENIDO Capítulo XVI. PRIMER
- Page 5 and 6: 12 FÍSICA. MAGNITUDES FÍSICAS. SI
- Page 7 and 8: 14 FÍSICA. MAGNITUDES FÍSICAS. SI
- Page 9 and 10: 16 FÍSICA. MAGNITUDES FÍSICAS. SI
- Page 11 and 12: 18 FÍSICA. MAGNITUDES FÍSICAS. SI
- Page 13 and 14: 20 FÍSICA. MAGNITUDES FÍSICAS. SI
- Page 15 and 16: 0 22 FÍSICA. MAGNITUDES FÍSICAS.
- Page 17 and 18: 24 FÍSICA. MAGNITUDES FÍSICAS. SI
- Page 19 and 20: 26 FÍSICA. MAGNITUDES FÍSICAS. SI
- Page 21 and 22: CAPÍTULO II CÁLCULO VECTORIAL. SI
- Page 23 and 24: VECTORES Y ESCALARES. SISTEMAS DE R
- Page 25 and 26: ÁLGEBRA VECTORIAL 33 y el módulo
- Page 27 and 28: ÁLGEBRA VECTORIAL 35 MUESTRA PARA
- Page 29 and 30: ÁLGEBRA VECTORIAL 37 c) Cuando dos
- Page 31 and 32: TEORÍA DE MOMENTOS 39 II - 20. Mom
- Page 33 and 34: TEORÍA DE MOMENTOS 41 Al conjunto
- Page 35 and 36: CÁLCULO INFINITESIMAL VECTORIAL 43
- Page 37 and 38: COORDENADAS POLARES 45 Desarrolland
- Page 39 and 40: MECÁNICA CAPÍTULO III CINEMÁTICA
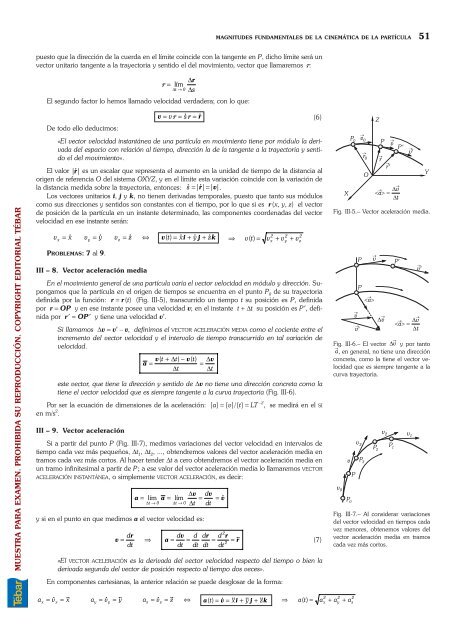
- Page 41: MAGNITUDES FUNDAMENTALES DE LA CINE
- Page 45 and 46: MOVIMIENTOS RECTILÍNEOS. MAGNITUDE
- Page 47 and 48: MOVIMIENTOS RECTILÍNEOS UNIFORME Y
- Page 49 and 50: OSCILACIONES 57 son equivalentes. L
- Page 51 and 52: OSCILACIONES 59 dará como resultan
- Page 53 and 54: OSCILACIONES 61 movimiento periódi
- Page 55 and 56: OSCILACIONES 63 A 0 : distancia má
- Page 57 and 58: PROBLEMAS 65 MUESTRA PARA EXAMEN. P
- Page 59 and 60: PROBLEMAS 67 MUESTRA PARA EXAMEN. P
- Page 61 and 62: CAPÍTULO IV CINEMÁTICA DE LOS MOV
- Page 63 and 64: MOVIMIENTOS CURVILÍNEOS DE LA PART
- Page 65 and 66: MUESTRA PARA EXAMEN. PROHIBIDA SU R
- Page 67 and 68: MOVIMIENTOS CURVILÍNEOS SINGULARES
- Page 69 and 70: COMPOSICIÓN DE MAS PERPENDICULARES
- Page 71 and 72: MOVIMIENTOS RELATIVOS 79 Esta dific
- Page 73 and 74: MOVIMIENTOS RELATIVOS 81 MUESTRA PA
- Page 75 and 76: PROBLEMAS 83 Fig. IV-22, y para el
- Page 77 and 78: PROBLEMAS 85 MUESTRA PARA EXAMEN. P
- Page 79 and 80: PROBLEMAS 87 MUESTRA PARA EXAMEN. P
- Page 81 and 82: DINÁMICA DE LA PARTÍCULA CAPÍTUL
- Page 83 and 84: PRIMERA LEY DE NEWTON. CONCEPTO DE
- Page 85 and 86: PRIMERA LEY DE NEWTON. CONCEPTO DE
- Page 87 and 88: PRIMERA LEY DE NEWTON. CONCEPTO DE
- Page 89 and 90: MOMENTO LINEAL. SEGUNDA Y TERCERA L
- Page 91 and 92: MAGNITUDES DINÁMICAS ANGULARES DE
- Page 93 and 94:
MAGNITUDES DINÁMICAS ANGULARES DE
- Page 95 and 96:
SISTEMAS NO INERCIALES. DINÁMICA D
- Page 97 and 98:
SISTEMAS NO INERCIALES. DINÁMICA D
- Page 99 and 100:
SISTEMAS NO INERCIALES. DINÁMICA D
- Page 101 and 102:
PROBLEMAS 109 nente F 1 forma un á
- Page 103 and 104:
PROBLEMAS 111 dos inferiores por un
- Page 105 and 106:
PROBLEMAS 113 62. Sobre un plano in
- Page 107 and 108:
MUESTRA PARA EXAMEN. PROHIBIDA SU R
- Page 109 and 110:
CAPÍTULO VI PESO. ROZAMIENTO. OSCI
- Page 111 and 112:
PESO. CENTRO DE GRAVEDAD 119 VI - 2
- Page 113 and 114:
ROZAMIENTO POR DESLIZAMIENTO 121 B)
- Page 115 and 116:
DINÁMICA DE LAS OSCILACIONES MECÁ
- Page 117 and 118:
DINÁMICA DE LAS OSCILACIONES MECÁ
- Page 119 and 120:
DINÁMICA DE LAS OSCILACIONES MECÁ
- Page 121 and 122:
PROBLEMAS 129 PROBLEMAS MUESTRA PAR
- Page 123 and 124:
PROBLEMAS 131 MUESTRA PARA EXAMEN.
- Page 125 and 126:
PROBLEMAS 133 un período de 2 s. C
- Page 127 and 128:
PROBLEMAS 135 MUESTRA PARA EXAMEN.
- Page 129 and 130:
138 TRABAJO Y ENERGÍA. TEORÍA DE
- Page 131 and 132:
140 TRABAJO Y ENERGÍA. TEORÍA DE
- Page 133 and 134:
142 TRABAJO Y ENERGÍA. TEORÍA DE
- Page 135 and 136:
144 TRABAJO Y ENERGÍA. TEORÍA DE
- Page 137 and 138:
146 TRABAJO Y ENERGÍA. TEORÍA DE
- Page 139 and 140:
148 TRABAJO Y ENERGÍA. TEORÍA DE
- Page 141 and 142:
150 TRABAJO Y ENERGÍA. TEORÍA DE
- Page 143 and 144:
152 TRABAJO Y ENERGÍA. TEORÍA DE
- Page 145 and 146:
154 TRABAJO Y ENERGÍA. TEORÍA DE
- Page 147 and 148:
156 TRABAJO Y ENERGÍA. TEORÍA DE
- Page 149 and 150:
158 TRABAJO Y ENERGÍA. TEORÍA DE
- Page 151 and 152:
TEORÍA - CAPÍTULO 07 - 3 as PRUEB
- Page 153 and 154:
TEORÍA - CAPÍTULO 07 - 3 as PRUEB
- Page 155 and 156:
TEORÍA - CAPÍTULO 07 - 3 as PRUEB
- Page 157 and 158:
DINÁMICA DE LOS SISTEMAS DE PARTÍ
- Page 159 and 160:
SISTEMAS DE PARTÍCULAS DISCRETOS 1
- Page 161 and 162:
SISTEMAS DE PARTÍCULAS DISCRETOS 1
- Page 163 and 164:
MAGNITUDES DINÁMICAS ANGULARES DE
- Page 165 and 166:
F HG d( v1 − v2) F12 F21 dv12 1 1
- Page 167 and 168:
ENERGÍA EN LOS SISTEMAS DE PARTÍC
- Page 169 and 170:
CHOQUE ENTRE PAREJAS DE PARTÍCULAS
- Page 171 and 172:
CHOQUE ENTRE PAREJAS DE PARTÍCULAS
- Page 173 and 174:
PROBLEMAS 183 que junto con el valo
- Page 175 and 176:
TEORÍA - CAPÍTULO 08 - 3 as PRUEB
- Page 177 and 178:
TEORÍA - CAPÍTULO 08 - 3 as PRUEB
- Page 179 and 180:
190 CINEMÁTICA Y ESTÁTICA DEL SÓ
- Page 181 and 182:
192 CINEMÁTICA Y ESTÁTICA DEL SÓ
- Page 183 and 184:
194 CINEMÁTICA Y ESTÁTICA DEL SÓ
- Page 185 and 186:
196 CINEMÁTICA Y ESTÁTICA DEL SÓ
- Page 187 and 188:
198 CINEMÁTICA Y ESTÁTICA DEL SÓ
- Page 189 and 190:
200 CINEMÁTICA Y ESTÁTICA DEL SÓ
- Page 191 and 192:
202 CINEMÁTICA Y ESTÁTICA DEL SÓ
- Page 193 and 194:
204 DINÁMICA DEL SÓLIDO RÍGIDO P
- Page 195 and 196:
206 DINÁMICA DEL SÓLIDO RÍGIDO a
- Page 197 and 198:
208 DINÁMICA DEL SÓLIDO RÍGIDO D
- Page 199 and 200:
210 DINÁMICA DEL SÓLIDO RÍGIDO d
- Page 201 and 202:
212 DINÁMICA DEL SÓLIDO RÍGIDO =
- Page 203 and 204:
214 DINÁMICA DEL SÓLIDO RÍGIDO q
- Page 205 and 206:
216 DINÁMICA DEL SÓLIDO RÍGIDO a
- Page 207 and 208:
218 DINÁMICA DEL SÓLIDO RÍGIDO F
- Page 209 and 210:
220 DINÁMICA DEL SÓLIDO RÍGIDO g
- Page 211 and 212:
222 DINÁMICA DEL SÓLIDO RÍGIDO (
- Page 213 and 214:
224 DINÁMICA DEL SÓLIDO RÍGIDO P
- Page 215 and 216:
226 DINÁMICA DEL SÓLIDO RÍGIDO 1
- Page 217 and 218:
228 EL CAMPO GRAVITATORIO Fig. XI-2
- Page 219 and 220:
230 EL CAMPO GRAVITATORIO DATOS TER
- Page 221 and 222:
232 EL CAMPO GRAVITATORIO XI - 6. E
- Page 223 and 224:
234 EL CAMPO GRAVITATORIO g g G M 0
- Page 225 and 226:
236 EL CAMPO GRAVITATORIO En efecto
- Page 227 and 228:
238 EL CAMPO GRAVITATORIO que susti
- Page 229 and 230:
240 EL CAMPO GRAVITATORIO por tanto
- Page 231 and 232:
242 EL CAMPO GRAVITATORIO M r = = 4
- Page 233 and 234:
244 EL CAMPO GRAVITATORIO 10R y se
- Page 235 and 236:
246 ESTUDIO BÁSICO DE LA ESTRUCTUR
- Page 237 and 238:
248 ESTUDIO BÁSICO DE LA ESTRUCTUR
- Page 239 and 240:
250 ESTUDIO BÁSICO DE LA ESTRUCTUR
- Page 241 and 242:
252 ESTUDIO BÁSICO DE LA ESTRUCTUR
- Page 243 and 244:
254 ESTUDIO BÁSICO DE LA ESTRUCTUR
- Page 245 and 246:
256 ESTUDIO BÁSICO DE LA ESTRUCTUR
- Page 247 and 248:
258 ESTUDIO BÁSICO DE LA ESTRUCTUR
- Page 249 and 250:
260 ESTUDIO BÁSICO DE LA ESTRUCTUR
- Page 251 and 252:
262 ESTUDIO BÁSICO DE LA ESTRUCTUR
- Page 253 and 254:
264 ESTUDIO BÁSICO DE LA ESTRUCTUR
- Page 255 and 256:
266 ESTUDIO BÁSICO DE LA ESTRUCTUR
- Page 257 and 258:
268 ESTUDIO BÁSICO DE LA ESTRUCTUR
- Page 259 and 260:
270 ESTUDIO BÁSICO DE LA ESTRUCTUR
- Page 261 and 262:
272 ESTUDIO BÁSICO DE LA ESTRUCTUR
- Page 263 and 264:
274 ESTUDIO BÁSICO DE LA ESTRUCTUR
- Page 265 and 266:
276 ESTUDIO BÁSICO DE LA ESTRUCTUR
- Page 267 and 268:
278 ESTUDIO BÁSICO DE LA ESTRUCTUR
- Page 269 and 270:
280 ESTUDIO BÁSICO DE LA ESTRUCTUR
- Page 271 and 272:
282 ESTUDIO BÁSICO DE LA ESTRUCTUR
- Page 273 and 274:
284 ELASTICIDAD. FENÓMENOS MOLÉCU
- Page 275 and 276:
286 ELASTICIDAD. FENÓMENOS MOLÉCU
- Page 277 and 278:
288 ELASTICIDAD. FENÓMENOS MOLÉCU
- Page 279 and 280:
290 ELASTICIDAD. FENÓMENOS MOLÉCU
- Page 281 and 282:
292 ELASTICIDAD. FENÓMENOS MOLÉCU
- Page 283 and 284:
294 ELASTICIDAD. FENÓMENOS MOLÉCU
- Page 285 and 286:
296 ELASTICIDAD. FENÓMENOS MOLÉCU
- Page 287 and 288:
298 TEMPERATURA Y DILATACIÓN. TEOR
- Page 289 and 290:
300 TEMPERATURA Y DILATACIÓN. TEOR
- Page 291 and 292:
302 TEMPERATURA Y DILATACIÓN. TEOR
- Page 293 and 294:
304 TEMPERATURA Y DILATACIÓN. TEOR
- Page 295 and 296:
306 TEMPERATURA Y DILATACIÓN. TEOR
- Page 297 and 298:
308 TEMPERATURA Y DILATACIÓN. TEOR
- Page 299 and 300:
310 TEMPERATURA Y DILATACIÓN. TEOR
- Page 301 and 302:
312 TEMPERATURA Y DILATACIÓN. TEOR
- Page 303 and 304:
314 TEMPERATURA Y DILATACIÓN. TEOR
- Page 305 and 306:
316 EL CALOR Y SUS EFECTOS CALORES
- Page 307 and 308:
318 EL CALOR Y SUS EFECTOS M ∆t M
- Page 309 and 310:
320 EL CALOR Y SUS EFECTOS Fig. XV-
- Page 311 and 312:
322 EL CALOR Y SUS EFECTOS Fig. XV-
- Page 313 and 314:
324 EL CALOR Y SUS EFECTOS MASA DE
- Page 315 and 316:
326 EL CALOR Y SUS EFECTOS XV - 34.
- Page 317 and 318:
328 EL CALOR Y SUS EFECTOS D) TRANS
- Page 319 and 320:
330 EL CALOR Y SUS EFECTOS Fig. XV-
- Page 321 and 322:
332 EL CALOR Y SUS EFECTOS n p = RT
- Page 323 and 324:
334 EL CALOR Y SUS EFECTOS Los gase
- Page 325 and 326:
336 EL CALOR Y SUS EFECTOS 38. Una
- Page 327 and 328:
338 PRIMER Y SEGUNDO PRINCIPIOS DE
- Page 329 and 330:
340 PRIMER Y SEGUNDO PRINCIPIOS DE
- Page 331 and 332:
342 PRIMER Y SEGUNDO PRINCIPIOS DE
- Page 333 and 334:
344 PRIMER Y SEGUNDO PRINCIPIOS DE
- Page 335 and 336:
346 PRIMER Y SEGUNDO PRINCIPIOS DE
- Page 337 and 338:
348 PRIMER Y SEGUNDO PRINCIPIOS DE
- Page 339 and 340:
350 PRIMER Y SEGUNDO PRINCIPIOS DE
- Page 341 and 342:
352 PRIMER Y SEGUNDO PRINCIPIOS DE
- Page 343 and 344:
354 PRIMER Y SEGUNDO PRINCIPIOS DE
- Page 345 and 346:
CAPÍTULO XVII ONDAS* XVII - 1. Mov
- Page 347 and 348:
ECUACIÓN DE ONDAS 359 Si llamamos
- Page 349 and 350:
ECUACIÓN DE ONDAS 361 También, se
- Page 351 and 352:
ENERGÍA E INTENSIDAD DE LAS ONDAS
- Page 353 and 354:
EFECTO DOPPLER-FIZEAU 365 MUESTRA P
- Page 355 and 356:
SUPERPOSICIÓN DE ONDAS. INTERFEREN
- Page 357 and 358:
SUPERPOSICIÓN DE ONDAS. INTERFEREN
- Page 359 and 360:
SUPERPOSICIÓN DE ONDAS. INTERFEREN
- Page 361 and 362:
L w2 − w1 k2 − k1 O L w2 + w1 k
- Page 363 and 364:
DIFRACCIÓN, REFLEXIÓN Y REFRACCI
- Page 365 and 366:
DIFRACCIÓN, REFLEXIÓN Y REFRACCI
- Page 367 and 368:
POLARIZACIÓN 379 CASOS PARTICULARE
- Page 369 and 370:
ACÚSTICA. PROPAGACIÓN DEL SONIDO
- Page 371 and 372:
CUALIDADES FÍSICAS DEL SONIDO 383
- Page 373 and 374:
INSTRUMENTOS MUSICALES 385 XVII - 3
- Page 375 and 376:
PERCEPCIÓN DEL SONIDO 387 nes de l
- Page 377 and 378:
PROBLEMAS 389 Un sonido tiene un ni
- Page 379 and 380:
PROBLEMAS 391 MUESTRA PARA EXAMEN.
- Page 381 and 382:
PROBLEMAS 393 74. Una sala tiene un
- Page 383 and 384:
396 ELECTROSTÁTICA Cuando un cuerp
- Page 385 and 386:
398 ELECTROSTÁTICA XVIII - 10. Car
- Page 387 and 388:
400 ELECTROSTÁTICA Pero cómo se
- Page 389 and 390:
402 ELECTROSTÁTICA esta magnitud a
- Page 391 and 392:
404 ELECTROSTÁTICA que aparece en
- Page 393 and 394:
406 ELECTROSTÁTICA si a esta ecuac
- Page 395 and 396:
408 ELECTROSTÁTICA Teniendo en cue
- Page 397 and 398:
410 ELECTROSTÁTICA V = V +zE ? dr
- Page 399 and 400:
412 ELECTROSTÁTICA XVIII - 32. Cá
- Page 401 and 402:
414 ELECTROSTÁTICA L NM 1 U q K q
- Page 403 and 404:
416 ELECTROSTÁTICA 17. Calcular la
- Page 405 and 406:
418 ELECTROSTÁTICA extremo, justam
- Page 407 and 408:
420 EL CAMPO ELÉCTRICO EN LA MATER
- Page 409 and 410:
422 EL CAMPO ELÉCTRICO EN LA MATER
- Page 411 and 412:
424 EL CAMPO ELÉCTRICO EN LA MATER
- Page 413 and 414:
426 EL CAMPO ELÉCTRICO EN LA MATER
- Page 415 and 416:
428 EL CAMPO ELÉCTRICO EN LA MATER
- Page 417 and 418:
430 EL CAMPO ELÉCTRICO EN LA MATER
- Page 419 and 420:
432 EL CAMPO ELÉCTRICO EN LA MATER
- Page 421 and 422:
434 EL CAMPO ELÉCTRICO EN LA MATER
- Page 423 and 424:
436 EL CAMPO ELÉCTRICO EN LA MATER
- Page 425 and 426:
438 EL CAMPO ELÉCTRICO EN LA MATER
- Page 427 and 428:
440 EL CAMPO ELÉCTRICO EN LA MATER
- Page 429 and 430:
442 EL CAMPO ELÉCTRICO EN LA MATER
- Page 431 and 432:
444 CORRIENTE ELÉCTRICA CONTINUA m
- Page 433 and 434:
446 CORRIENTE ELÉCTRICA CONTINUA e
- Page 435 and 436:
448 CORRIENTE ELÉCTRICA CONTINUA R
- Page 437 and 438:
450 CORRIENTE ELÉCTRICA CONTINUA L
- Page 439 and 440:
452 CORRIENTE ELÉCTRICA CONTINUA V
- Page 441 and 442:
454 CORRIENTE ELÉCTRICA CONTINUA R
- Page 443 and 444:
456 CORRIENTE ELÉCTRICA CONTINUA X
- Page 445 and 446:
458 CORRIENTE ELÉCTRICA CONTINUA F
- Page 447 and 448:
460 CORRIENTE ELÉCTRICA CONTINUA 2
- Page 449 and 450:
462 CORRIENTE ELÉCTRICA CONTINUA T
- Page 451 and 452:
464 CORRIENTE ELÉCTRICA CONTINUA A
- Page 453 and 454:
466 CORRIENTE ELÉCTRICA CONTINUA F
- Page 455 and 456:
468 CORRIENTE ELÉCTRICA CONTINUA p
- Page 457 and 458:
470 CORRIENTE ELÉCTRICA CONTINUA t
- Page 459 and 460:
472 CORRIENTE ELÉCTRICA CONTINUA h
- Page 461 and 462:
CAPÍTULO XXI EL CAMPO MAGNÉTICO A
- Page 463 and 464:
INTRODUCCIÓN 477 MUESTRA PARA EXAM
- Page 465 and 466:
Idl FUERZA DE LORENTZ: APLICACIONES
- Page 467 and 468:
FUERZA DE LORENTZ: APLICACIONES 481
- Page 469 and 470:
FUERZA DE LORENTZ: APLICACIONES 483
- Page 471 and 472:
LEY DE BIOT Y SAVART: APLICACIONES
- Page 473 and 474:
LEY DE BIOT Y SAVART: APLICACIONES
- Page 475 and 476:
LEY DE BIOT Y SAVART: APLICACIONES
- Page 477 and 478:
XXI - 26. Ley de Ampère «En un ca
- Page 479 and 480:
que igualada a la anterior, nos que
- Page 481 and 482:
PROPIEDADES MAGNÉTICAS DE LA MATER
- Page 483 and 484:
PROPIEDADES MAGNÉTICAS DE LA MATER
- Page 485 and 486:
PROPIEDADES MAGNÉTICAS DE LA MATER
- Page 487 and 488:
PROPIEDADES MAGNÉTICAS DE LA MATER
- Page 489 and 490:
PROPIEDADES MAGNÉTICAS DE LA MATER
- Page 491 and 492:
PROPIEDADES MAGNÉTICAS DE LA MATER
- Page 493 and 494:
APARATOS DE LA MEDIDA DE CORRIENTE
- Page 495 and 496:
PROBLEMAS 509 MUESTRA PARA EXAMEN.
- Page 497 and 498:
PROBLEMAS 511 MUESTRA PARA EXAMEN.
- Page 499 and 500:
CAPÍTULO XXII CORRIENTES INDUCIDAS
- Page 501 and 502:
LEYES DE FARADAY Y DE LENZ 515 MUES
- Page 503 and 504:
AUTOINDUCCIÓN E INDUCCIÓN ENTRE C
- Page 505 and 506:
AUTOINDUCCIÓN E INDUCCIÓN ENTRE C
- Page 507 and 508:
ENERGÍA MAGNÉTICA. DESCARGA OSCIL
- Page 509 and 510:
ENERGÍA MAGNÉTICA. DESCARGA OSCIL
- Page 511 and 512:
CORRIENTES ALTERNAS: PRODUCCIÓN. E
- Page 513 and 514:
ESTUDIO DEL CIRCUITO BÁSICO DE COR
- Page 515 and 516:
INTENSIDAD Y FEM EFICACES. POTENCIA
- Page 517 and 518:
INTENSIDAD Y FEM EFICACES. POTENCIA
- Page 519 and 520:
FENÓMENOS DE RESONANCIA 533 das la
- Page 521 and 522:
AMPERÍMETROS, VOLTÍMETROS Y VATÍ
- Page 523 and 524:
MÁQUINAS ELÉCTRICAS. GENERADORES
- Page 525 and 526:
GENERADORES DE CORRIENTE CONTINUA 5
- Page 527 and 528:
ELECTROMOTORES 541 circular por las
- Page 529 and 530:
TRANSFORMADORES 543 MUESTRA PARA EX
- Page 531 and 532:
PROBLEMAS 545 MUESTRA PARA EXAMEN.
- Page 533 and 534:
PROBLEMAS 547 MUESTRA PARA EXAMEN.
- Page 535 and 536:
PROBLEMAS 549 MUESTRA PARA EXAMEN.
- Page 537 and 538:
552 ECUACIONES DE MAXWELL. ONDAS EL
- Page 539 and 540:
554 ECUACIONES DE MAXWELL. ONDAS EL
- Page 541 and 542:
556 ECUACIONES DE MAXWELL. ONDAS EL
- Page 543 and 544:
558 ECUACIONES DE MAXWELL. ONDAS EL
- Page 545 and 546:
560 ECUACIONES DE MAXWELL. ONDAS EL
- Page 547 and 548:
562 ECUACIONES DE MAXWELL. ONDAS EL
- Page 549 and 550:
564 ECUACIONES DE MAXWELL. ONDAS EL
- Page 551 and 552:
566 ECUACIONES DE MAXWELL. ONDAS EL
- Page 553 and 554:
ÓPTICA CAPÍTULO XXIV ÓPTICA GEOM
- Page 555 and 556:
PROPAGACIÓN DE LA LUZ, REFLEXIÓN
- Page 557 and 558:
PROPAGACIÓN DE LA LUZ, REFLEXIÓN
- Page 559 and 560:
PROPAGACIÓN DE LA LUZ, REFLEXIÓN
- Page 561 and 562:
PROPAGACIÓN DE LA LUZ, REFLEXIÓN
- Page 563 and 564:
PRISMA ÓPTICO 579 e′ + e′ = a
- Page 565 and 566:
DIOPTRIO ESFÉRICO 581 por s); pudi
- Page 567 and 568:
ESPEJOS 583 y b = ′ s =− ′ f
- Page 569 and 570:
ESPEJOS 585 · d d = 360 − 2 ( e
- Page 571 and 572:
PROBLEMAS 587 La imagen está situa
- Page 573 and 574:
PROBLEMAS 589 MUESTRA PARA EXAMEN.
- Page 575 and 576:
592 ÓPTICA GEOMÉTRICA II En conse
- Page 577 and 578:
594 ÓPTICA GEOMÉTRICA II Fig. XXV
- Page 579 and 580:
596 ÓPTICA GEOMÉTRICA II D =−5r
- Page 581 and 582:
598 ÓPTICA GEOMÉTRICA II XXV - 21
- Page 583 and 584:
600 ÓPTICA GEOMÉTRICA II Fig. XXV
- Page 585 and 586:
602 ÓPTICA GEOMÉTRICA II es hiper
- Page 587 and 588:
604 ÓPTICA GEOMÉTRICA II En tales
- Page 589 and 590:
606 ÓPTICA GEOMÉTRICA II La pupil
- Page 591 and 592:
608 ÓPTICA GEOMÉTRICA II 19. Sea
- Page 593 and 594:
610 ÓPTICA GEOMÉTRICA II rayos,
- Page 595 and 596:
612 ÓPTICA FÍSICA mina, formando
- Page 597 and 598:
614 ÓPTICA FÍSICA Los cuerpos pro
- Page 599 and 600:
616 ÓPTICA FÍSICA RAYA A B C D E
- Page 601 and 602:
618 ÓPTICA FÍSICA Fig. XXVI-13.-
- Page 603 and 604:
620 ÓPTICA FÍSICA Fig. XXVI-16.-
- Page 605 and 606:
622 ÓPTICA FÍSICA VALORES DE LA L
- Page 607 and 608:
624 ÓPTICA FÍSICA La CANDELA (cd)
- Page 609 and 610:
626 ÓPTICA FÍSICA Fig. XXVI-26.-
- Page 611 and 612:
628 ÓPTICA FÍSICA Los puntos de l
- Page 613 and 614:
630 ÓPTICA FÍSICA eléctrico y de
- Page 615 and 616:
632 ÓPTICA FÍSICA La diferencia d
- Page 617 and 618:
634 ÓPTICA FÍSICA Fig. XXVI-45.-
- Page 619 and 620:
636 ÓPTICA FÍSICA XXVI - 37. Pode
- Page 621 and 622:
638 ÓPTICA FÍSICA XXVI - 40. Disp
- Page 623 and 624:
640 ÓPTICA FÍSICA Si en vez de ai
- Page 625 and 626:
642 ÓPTICA FÍSICA Fig. XXVI-66.-
- Page 627 and 628:
644 ÓPTICA FÍSICA Fig. XXVI-71.-
- Page 629 and 630:
646 ÓPTICA FÍSICA jo luminoso tot
- Page 631 and 632:
RELATIVIDAD CAPÍTULO XXVII CINEMÁ
- Page 633 and 634:
CINEMÁTICA RELATIVISTA 651 y al se
- Page 635 and 636:
CINEMÁTICA RELATIVISTA 653 XXVII -
- Page 637 and 638:
CINEMÁTICA RELATIVISTA 655 x′
- Page 639 and 640:
CINEMÁTICA RELATIVISTA 657 como el
- Page 641 and 642:
DINÁMICA RELATIVISTA 659 B) DINÁM
- Page 643 and 644:
DINÁMICA RELATIVISTA 661 y, operan
- Page 645 and 646:
DINÁMICA RELATIVISTA 663 «Toda ma
- Page 647 and 648:
PROBLEMAS 665 Este enunciado consti
- Page 649 and 650:
PROBLEMAS 667 MUESTRA PARA EXAMEN.
- Page 651 and 652:
670 CORTEZA ATÓMICA Fig. XXVIII-2.
- Page 653 and 654:
672 CORTEZA ATÓMICA lidad. Si a un
- Page 655 and 656:
674 CORTEZA ATÓMICA compacto de es
- Page 657 and 658:
676 CORTEZA ATÓMICA que comparada
- Page 659 and 660:
678 CORTEZA ATÓMICA XXVIII - 12. E
- Page 661 and 662:
680 CORTEZA ATÓMICA electrón una
- Page 663 and 664:
682 CORTEZA ATÓMICA m l =+ 1 SUBNI
- Page 665 and 666:
684 CORTEZA ATÓMICA MUESTRA PARA E
- Page 667 and 668:
686 CORTEZA ATÓMICA XXVIII - 19. D
- Page 669 and 670:
688 CORTEZA ATÓMICA XXVIII - 24. P
- Page 671 and 672:
690 CORTEZA ATÓMICA Fig. XXVIII-36
- Page 673 and 674:
692 CORTEZA ATÓMICA Los rayos X de
- Page 675 and 676:
694 CORTEZA ATÓMICA XXVIII - 35. L
- Page 677 and 678:
696 CORTEZA ATÓMICA y por ser p =
- Page 679 and 680:
698 CORTEZA ATÓMICA el campo eléc
- Page 681 and 682:
700 CORTEZA ATÓMICA = cos a ± i s
- Page 683 and 684:
702 CORTEZA ATÓMICA 19. Un haz de
- Page 685 and 686:
704 ELECTRÓNICA Los electrones só
- Page 687 and 688:
706 ELECTRÓNICA El EFECTO SCHOTTKY
- Page 689 and 690:
708 ELECTRÓNICA la diferencia de p
- Page 691 and 692:
710 ELECTRÓNICA Fig. XXIX-24.- Cor
- Page 693 and 694:
712 ELECTRÓNICA Fig. XXIX-32.- Tri
- Page 695 and 696:
714 ELECTRÓNICA La CÉLULA DE HIER
- Page 697 and 698:
716 ELECTRÓNICA Fig. XXIX-47.- Fun
- Page 699 and 700:
718 ELECTRÓNICA Fig. XXIX-52.- a)
- Page 701 and 702:
720 ELECTRÓNICA Fig. XXIX-60.- En
- Page 703 and 704:
722 ELECTRÓNICA Si representamos l
- Page 705 and 706:
724 ELECTRÓNICA B) La función NI.
- Page 707 and 708:
726 ELECTRÓNICA de colector median
- Page 709 and 710:
728 EL NÚCLEO ATÓMICO El valor ex
- Page 711 and 712:
730 EL NÚCLEO ATÓMICO Fig. XXX-6.
- Page 713 and 714:
732 EL NÚCLEO ATÓMICO 1s de los n
- Page 715 and 716:
734 EL NÚCLEO ATÓMICO cambia ni e
- Page 717 and 718:
736 EL NÚCLEO ATÓMICO XXX - 16. P
- Page 719 and 720:
738 EL NÚCLEO ATÓMICO Fig. XXX-18
- Page 721 and 722:
740 EL NÚCLEO ATÓMICO reactivos,
- Page 723 and 724:
742 EL NÚCLEO ATÓMICO Fig. XXX-24
- Page 725 and 726:
744 EL NÚCLEO ATÓMICO En la actua
- Page 727 and 728:
746 EL NÚCLEO ATÓMICO Fig. XXX-28
- Page 729 and 730:
748 EL NÚCLEO ATÓMICO ese número
- Page 731 and 732:
750 EL NÚCLEO ATÓMICO Fig. XXX-36
- Page 733 and 734:
752 EL NÚCLEO ATÓMICO Fig. XXX-40
- Page 735 and 736:
754 EL NÚCLEO ATÓMICO producido,
- Page 737 and 738:
756 EL NÚCLEO ATÓMICO La suma de
- Page 739 and 740:
758 EL NÚCLEO ATÓMICO ner tres co
- Page 741 and 742:
760 EL NÚCLEO ATÓMICO electrón s
- Page 743 and 744:
SIMBOLOGÍA Y NOMENCLATURA UTILIZAD
- Page 745 and 746:
SIMBOLOGÍA Y NOMENCLATURA UTILIZAD
- Page 747:
SIMBOLOGÍA Y NOMENCLATURA UTILIZAD