- Seite 1 und 2:
Klenke Wahrscheinlichkeitstheorie
- Seite 3 und 4:
Prof. Dr. Achim Klenke Institut fü
- Seite 5 und 6:
VI Vorwort In den ersten acht Kapit
- Seite 7 und 8:
VIII Inhaltsverzeichnis 5.3 Starkes
- Seite 9 und 10:
X Inhaltsverzeichnis 17.1 Begriffsb
- Seite 11 und 12:
XII Inhaltsverzeichnis Literatur...
- Seite 13 und 14:
2 1 Grundlagen der Maßtheorie Defi
- Seite 15 und 16:
4 1 Grundlagen der Maßtheorie Defi
- Seite 17 und 18:
6 1 Grundlagen der Maßtheorie Satz
- Seite 19 und 20:
8 1 Grundlagen der Maßtheorie Nach
- Seite 21 und 22:
10 1 Grundlagen der Maßtheorie Bew
- Seite 23 und 24:
12 1 Grundlagen der Maßtheorie (v)
- Seite 25 und 26:
14 1 Grundlagen der Maßtheorie Bew
- Seite 27 und 28:
16 1 Grundlagen der Maßtheorie Sat
- Seite 29 und 30:
18 1 Grundlagen der Maßtheorie Bei
- Seite 31 und 32:
20 1 Grundlagen der Maßtheorie (ii
- Seite 33 und 34:
22 1 Grundlagen der Maßtheorie U(A
- Seite 35 und 36:
24 1 Grundlagen der Maßtheorie Bew
- Seite 37 und 38:
26 1 Grundlagen der Maßtheorie Bei
- Seite 39 und 40:
28 1 Grundlagen der Maßtheorie Mes
- Seite 41 und 42:
30 1 Grundlagen der Maßtheorie Bew
- Seite 43 und 44:
32 1 Grundlagen der Maßtheorie Def
- Seite 45 und 46:
34 1 Grundlagen der Maßtheorie Bei
- Seite 47 und 48:
36 1 Grundlagen der Maßtheorie Wir
- Seite 49 und 50:
38 1 Grundlagen der Maßtheorie Ana
- Seite 51 und 52:
40 1 Grundlagen der Maßtheorie (ii
- Seite 53 und 54:
42 1 Grundlagen der Maßtheorie (i)
- Seite 55 und 56:
44 1 Grundlagen der Maßtheorie so
- Seite 57 und 58:
46 1 Grundlagen der Maßtheorie Bei
- Seite 59 und 60:
48 2 Unabhängigkeit Wir prüfen je
- Seite 61 und 62:
50 2 Unabhängigkeit � � P j∈
- Seite 63 und 64:
52 2 Unabhängigkeit (ii) Offensich
- Seite 65 und 66:
54 2 Unabhängigkeit (iii) ” =⇒
- Seite 67 und 68:
56 2 Unabhängigkeit Xn : Ω → E,
- Seite 69 und 70:
58 2 Unabhängigkeit FY (x) =P �
- Seite 71 und 72:
60 2 Unabhängigkeit Beweis. Für j
- Seite 73 und 74:
62 2 Unabhängigkeit Beweis. ”
- Seite 75 und 76:
64 2 Unabhängigkeit Beweis. Sei X
- Seite 77 und 78:
66 2 Unabhängigkeit � � �
- Seite 79 und 80:
68 2 Unabhängigkeit Aufgrund der M
- Seite 81 und 82:
70 2 Unabhängigkeit 1 0 −1 �
- Seite 83 und 84:
72 2 Unabhängigkeit 2. Schritt Wir
- Seite 85 und 86:
74 2 Unabhängigkeit von Kanten k
- Seite 87 und 88:
76 3 Erzeugendenfunktion (ii) Die V
- Seite 89 und 90:
78 3 Erzeugendenfunktion � � α
- Seite 91 und 92:
80 3 Erzeugendenfunktion also ψSn(
- Seite 93 und 94:
82 3 Erzeugendenfunktion Satz 3.11
- Seite 95 und 96:
84 4 Das Integral m� m� n� α
- Seite 97 und 98:
86 4 Das Integral fn ↑ f und gn
- Seite 99 und 100:
88 4 Das Integral Zu (a): Es ist (f
- Seite 101 und 102:
90 4 Das Integral Satz 4.17. Die Ab
- Seite 103 und 104:
92 4 Das Integral Beispiel 4.22 (Pe
- Seite 105 und 106:
94 4 Das Integral Satz 4.23 (Rieman
- Seite 107 und 108:
96 4 Das Integral Hieraus folgt (4.
- Seite 109 und 110:
98 5 Momente und Gesetze der Große
- Seite 111 und 112:
100 5 Momente und Gesetze der Groß
- Seite 113 und 114:
102 5 Momente und Gesetze der Groß
- Seite 115 und 116:
104 5 Momente und Gesetze der Groß
- Seite 117 und 118:
106 5 Momente und Gesetze der Groß
- Seite 119 und 120:
108 5 Momente und Gesetze der Groß
- Seite 121 und 122:
110 5 Momente und Gesetze der Groß
- Seite 123 und 124:
112 5 Momente und Gesetze der Groß
- Seite 125 und 126:
114 5 Momente und Gesetze der Groß
- Seite 127 und 128:
116 5 Momente und Gesetze der Groß
- Seite 129 und 130:
118 5 Momente und Gesetze der Groß
- Seite 131 und 132:
120 5 Momente und Gesetze der Groß
- Seite 133 und 134:
122 5 Momente und Gesetze der Groß
- Seite 135 und 136:
6 Konvergenzsätze Im starken und s
- Seite 137 und 138:
6.1 Fast-überall- und stochastisch
- Seite 139 und 140:
6.1 Fast-überall- und stochastisch
- Seite 141 und 142:
6.2 Gleichgradige Integrierbarkeit
- Seite 143 und 144:
6.2 Gleichgradige Integrierbarkeit
- Seite 145 und 146:
Beweis. ” (i) =⇒ (ii)“ Dies i
- Seite 147 und 148:
6.3 Vertauschung von Integral und A
- Seite 149 und 150:
7 L p -Räume und Satz von Radon-Ni
- Seite 151 und 152:
7.2 Ungleichungen und Satz von Fisc
- Seite 153 und 154:
7.2 Ungleichungen und Satz von Fisc
- Seite 155 und 156:
7.2 Ungleichungen und Satz von Fisc
- Seite 157 und 158:
7.3 Hilberträume 147 wobei wir im
- Seite 159 und 160:
7.3 Hilberträume 149 Da V vollstä
- Seite 161 und 162:
7.4 Lebesgue’scher Zerlegungssatz
- Seite 163 und 164:
7.4 Lebesgue’scher Zerlegungssatz
- Seite 165 und 166:
7.5 Ergänzung: Signierte Maße 155
- Seite 167 und 168:
7.5 Ergänzung: Signierte Maße 157
- Seite 169 und 170:
7.5 Ergänzung: Signierte Maße 159
- Seite 171 und 172:
V ′ := {F : V → R ist stetig un
- Seite 173 und 174:
7.6 Ergänzung: Dualräume 163 Beme
- Seite 175 und 176:
166 8 Bedingte Erwartungen Durch da
- Seite 177 und 178:
168 8 Bedingte Erwartungen Offenbar
- Seite 179 und 180:
170 8 Bedingte Erwartungen Satz 8.1
- Seite 181 und 182:
172 8 Bedingte Erwartungen Korollar
- Seite 183 und 184:
174 8 Bedingte Erwartungen Tat: Sei
- Seite 185 und 186:
176 8 Bedingte Erwartungen Bemerkun
- Seite 187 und 188:
178 8 Bedingte Erwartungen Beispiel
- Seite 189 und 190:
180 8 Bedingte Erwartungen Ein sepa
- Seite 191 und 192:
182 8 Bedingte Erwartungen Übung 8
- Seite 193 und 194:
184 9 Martingale E = Z (mit der dis
- Seite 195 und 196:
186 9 Martingale F = σ(D). Wir int
- Seite 197 und 198:
188 9 Martingale Definition 9.22. I
- Seite 199 und 200:
190 9 Martingale Beispiel 9.31. Wir
- Seite 201 und 202:
192 9 Martingale Übung 9.2.4 (Ungl
- Seite 203 und 204:
194 9 Martingale vorhersagbar und l
- Seite 205 und 206:
196 9 Martingale Wir wollen nun X a
- Seite 207 und 208:
10 Optional Sampling Sätze Wir hab
- Seite 209 und 210:
10.1 Doob-Zerlegung und quadratisch
- Seite 211 und 212:
10.2 Optional Sampling und Optional
- Seite 213 und 214:
10.2 Optional Sampling und Optional
- Seite 215 und 216:
10.3 Gleichgradige Integrierbarkeit
- Seite 217 und 218:
11 Martingalkonvergenzsätze und An
- Seite 219 und 220:
E � (|X| ∗ n ∧ K) p� ≤ 11
- Seite 221 und 222:
und C = � a,b∈Q a
- Seite 223 und 224:
11.2 Martingalkonvergenzsätze 215
- Seite 225 und 226:
11.2 Martingalkonvergenzsätze 217
- Seite 227 und 228:
11.3 Beispiel: Verzweigungsprozess
- Seite 229 und 230:
12 Rückwärtsmartingale und Austau
- Seite 231 und 232:
12.1 Austauschbare Familien von Zuf
- Seite 233 und 234:
12.1 Austauschbare Familien von Zuf
- Seite 235 und 236:
1 n n� i=1 Xi In der Tat: Setzen
- Seite 237 und 238:
12.3 Satz von de Finetti 229 Defini
- Seite 239 und 240:
12.3 Satz von de Finetti 231 das he
- Seite 241 und 242:
13 Konvergenz von Maßen In der Wah
- Seite 243 und 244:
13.1 Wiederholung Topologie 235 Def
- Seite 245 und 246:
13.1 Wiederholung Topologie 237 Da
- Seite 247 und 248:
13.1 Wiederholung Topologie 239 Üb
- Seite 249 und 250:
13.2 Schwache und vage Konvergenz 2
- Seite 251 und 252:
13.2 Schwache und vage Konvergenz 2
- Seite 253 und 254:
13.2 Schwache und vage Konvergenz 2
- Seite 255 und 256:
13.2 Schwache und vage Konvergenz 2
- Seite 257 und 258:
13.3 Der Satz von Prohorov 249 Satz
- Seite 259 und 260:
13.3 Der Satz von Prohorov 251 besi
- Seite 261 und 262:
13.3 Der Satz von Prohorov 253 �
- Seite 263 und 264:
13.3 Der Satz von Prohorov 255 1. S
- Seite 265 und 266:
13.4 Anwendung: Satz von de Finetti
- Seite 267 und 268:
14 W-Maße auf Produkträumen Als M
- Seite 269 und 270:
14.1 Produkträume 261 Definition 1
- Seite 271 und 272:
14.2 Endliche Produkte und Übergan
- Seite 273 und 274:
14.2 Endliche Produkte und Übergan
- Seite 275 und 276:
14.2 Endliche Produkte und Übergan
- Seite 277 und 278:
14.2 Endliche Produkte und Übergan
- Seite 279 und 280:
14.2 Endliche Produkte und Übergan
- Seite 281 und 282:
14.3 Satz von Ionescu-Tulcea und Pr
- Seite 283 und 284:
14.3 Satz von Ionescu-Tulcea und Pr
- Seite 285 und 286:
14.4 Markov’sche Halbgruppen 277
- Seite 287 und 288:
14.4 Markov’sche Halbgruppen 279
- Seite 289 und 290:
15 Charakteristische Funktion und Z
- Seite 291 und 292:
15.1 Trennende Funktionenklassen 28
- Seite 293 und 294:
15.1 Trennende Funktionenklassen 28
- Seite 295 und 296:
15.1 Trennende Funktionenklassen 28
- Seite 297 und 298:
15.2 Charakteristische Funktionen:
- Seite 299 und 300:
15.2 Charakteristische Funktionen:
- Seite 301 und 302:
ϕμ(t) = 15.2 Charakteristische Fu
- Seite 303 und 304:
15.3 Der Lévy’sche Stetigkeitssa
- Seite 305 und 306:
15.3 Der Lévy’sche Stetigkeitssa
- Seite 307 und 308:
15.4 Charakteristische Funktion und
- Seite 309 und 310:
� � � �ϕ(t + h) − � n
- Seite 311 und 312:
15.4 Charakteristische Funktion und
- Seite 313 und 314:
15.5 Der Zentrale Grenzwertsatz 305
- Seite 315 und 316:
15.5 Der Zentrale Grenzwertsatz 307
- Seite 317 und 318:
Beweis. Für jedes n ∈ N ist νn
- Seite 319 und 320:
15.5 Der Zentrale Grenzwertsatz 311
- Seite 321 und 322:
15.6 Mehrdimensionaler Zentraler Gr
- Seite 323 und 324:
316 16 Unbegrenzt teilbare Verteilu
- Seite 325 und 326:
318 16 Unbegrenzt teilbare Verteilu
- Seite 327 und 328:
320 16 Unbegrenzt teilbare Verteilu
- Seite 329 und 330:
322 16 Unbegrenzt teilbare Verteilu
- Seite 331 und 332:
324 16 Unbegrenzt teilbare Verteilu
- Seite 333 und 334:
326 16 Unbegrenzt teilbare Verteilu
- Seite 335 und 336:
328 16 Unbegrenzt teilbare Verteilu
- Seite 337 und 338:
330 16 Unbegrenzt teilbare Verteilu
- Seite 339 und 340:
17 Markovketten Markovprozesse mit
- Seite 341 und 342:
17.1 Begriffsbildung und Konstrukti
- Seite 343 und 344:
Ex 17.1 Begriffsbildung und Konstru
- Seite 345 und 346:
17.1 Begriffsbildung und Konstrukti
- Seite 347 und 348:
17.2 Diskrete Markovketten, Beispie
- Seite 349 und 350:
17.2 Diskrete Markovketten, Beispie
- Seite 351 und 352:
17.3 Diskrete Markovprozesse in ste
- Seite 353 und 354:
Schreiben wir 17.3 Diskrete Markovp
- Seite 355 und 356:
17.4 Diskrete Markovketten, Rekurre
- Seite 357 und 358:
1 17.4 Diskrete Markovketten, Rekur
- Seite 359 und 360:
17.5 Anwendung: Rekurrenz und Trans
- Seite 361 und 362:
17.5 Anwendung: Rekurrenz und Trans
- Seite 363 und 364:
17.5 Anwendung: Rekurrenz und Trans
- Seite 365 und 366:
17.5 Anwendung: Rekurrenz und Trans
- Seite 367 und 368:
17.6 Invariante Verteilungen 361 Sa
- Seite 369 und 370:
17.6 Invariante Verteilungen 363 Sa
- Seite 371 und 372:
18 Konvergenz von Markovketten Wir
- Seite 373 und 374:
3 1/2 1/2 2 1 1 18.1 Periodizität
- Seite 375 und 376:
18.2 Kopplung und Konvergenzsatz 36
- Seite 377 und 378:
18.2 Kopplung und Konvergenzsatz 37
- Seite 379 und 380:
18.2 Kopplung und Konvergenzsatz 37
- Seite 381 und 382:
18.2 Kopplung und Konvergenzsatz 37
- Seite 383 und 384:
18.3 Markovketten Monte Carlo Metho
- Seite 385 und 386:
1 0.8 0.6 0.4 0.2 Magnetisierung 18
- Seite 387 und 388:
18.3 Markovketten Monte Carlo Metho
- Seite 389 und 390:
18.4 Konvergenzgeschwindigkeit 383
- Seite 391 und 392: 18.4 Konvergenzgeschwindigkeit 385
- Seite 393 und 394: Dabei ist die Varianz des einzelnen
- Seite 395 und 396: 19 Markovketten und elektrische Net
- Seite 397 und 398: 19.1 Harmonische Funktionen 391 Die
- Seite 399 und 400: 19.3 Elektrische Netzwerke 393 Defi
- Seite 401 und 402: 19.3 Elektrische Netzwerke 395 und
- Seite 403 und 404: x =0 0 u(0)=0 R R R R R R 1 2 3 4 5
- Seite 405 und 406: 19.4 Rekurrenz und Transienz 19.4 R
- Seite 407 und 408: 19.4 Rekurrenz und Transienz 401 Be
- Seite 409 und 410: 19.4 Rekurrenz und Transienz 403 -
- Seite 411 und 412: Also ist R ′ eff(0 ↔∞)= 1 3
- Seite 413 und 414: Schritt 1. Die Schleife am rechten
- Seite 415 und 416: Alternative Lösung 19.5 Netzwerkre
- Seite 417 und 418: Übung 19.5.3. Man betrachte den Gr
- Seite 419 und 420: 19.6 Irrfahrt in zufälliger Umgebu
- Seite 421 und 422: 20 Ergodentheorie Gesetze der groß
- Seite 423 und 424: 20.1 Begriffsbildung 417 Beispiel 2
- Seite 425 und 426: 20.2 Ergodensätze 419 Daher ist X0
- Seite 427 und 428: Beweis. Setze Yn := � � � n
- Seite 429 und 430: 20.4 Anwendung: Rekurrenz von Irrfa
- Seite 431 und 432: 20.4 Anwendung: Rekurrenz von Irrfa
- Seite 433 und 434: 1 lim n→∞ n 20.5 Mischung 427 n
- Seite 435 und 436: 21 Die Brown’sche Bewegung In Bei
- Seite 437 und 438: 21.1 Stetige Modifikationen 431 Fü
- Seite 439 und 440: 21.1 Stetige Modifikationen 433 s
- Seite 441: 21.1 Stetige Modifikationen 435 Üb
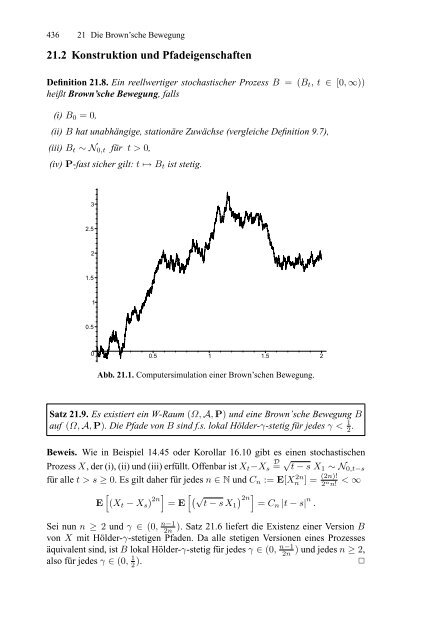
- Seite 445 und 446: 21.2 Konstruktion und Pfadeigenscha
- Seite 447 und 448: 21.3 Starke Markoveigenschaft 441
- Seite 449 und 450: 21.3 Starke Markoveigenschaft 443 B
- Seite 451 und 452: 21.4 Ergänzung: Feller Prozesse 44
- Seite 453 und 454: 21.5 Konstruktion durch L 2 -Approx
- Seite 455 und 456: X n := 21.5 Konstruktion durch L 2
- Seite 457 und 458: 21.6 Der Raum C([0, ∞)) 451 Übun
- Seite 459 und 460: 21.7 Konvergenz von W-Maßen auf C(
- Seite 461 und 462: 21.7 Konvergenz von W-Maßen auf C(
- Seite 463 und 464: 21.8 Satz von Donsker 457 Satz 21.4
- Seite 465 und 466: E � ( ¯ T Kn,n t+s − ¯ T Kn,n
- Seite 467 und 468: und induktiv 21.9 Pfadweise Konverg
- Seite 469 und 470: 21.9 Pfadweise Konvergenz von Verzw
- Seite 471 und 472: 21.10 Quadratische Variation und lo
- Seite 473 und 474: 21.10 Quadratische Variation und lo
- Seite 475 und 476: 21.10 Quadratische Variation und lo
- Seite 477 und 478: 21.10 Quadratische Variation und lo
- Seite 479 und 480: 21.10 Quadratische Variation und lo
- Seite 481 und 482: 21.10 Quadratische Variation und lo
- Seite 483 und 484: 22 Gesetz vom iterierten Logarithmu
- Seite 485 und 486: 22.1 Iterierter Logarithmus für di
- Seite 487 und 488: 22.2 Skorohod’scher Einbettungssa
- Seite 489 und 490: Für n ∈ N und σ ∈{−, +} n s
- Seite 491 und 492: 22.2 Skorohod’scher Einbettungssa
- Seite 493 und 494:
M ′ n := sup |Bs − Btn−1 s∈
- Seite 495 und 496:
490 23 Große Abweichungen 23.1 Sat
- Seite 497 und 498:
492 23 Große Abweichungen Beweis.
- Seite 499 und 500:
494 23 Große Abweichungen Λ ∗ (
- Seite 501 und 502:
496 23 Große Abweichungen Beweis.
- Seite 503 und 504:
498 23 Große Abweichungen Übung 2
- Seite 505 und 506:
500 23 Große Abweichungen Seien nu
- Seite 507 und 508:
502 23 Große Abweichungen Analog i
- Seite 509 und 510:
504 23 Große Abweichungen Untere S
- Seite 511 und 512:
506 23 Große Abweichungen 0.01 0.0
- Seite 513 und 514:
508 23 Große Abweichungen Im Fall
- Seite 515 und 516:
510 24 Der Poisson’sche Punktproz
- Seite 517 und 518:
512 24 Der Poisson’sche Punktproz
- Seite 519 und 520:
514 24 Der Poisson’sche Punktproz
- Seite 521 und 522:
516 24 Der Poisson’sche Punktproz
- Seite 523 und 524:
518 24 Der Poisson’sche Punktproz
- Seite 525 und 526:
520 24 Der Poisson’sche Punktproz
- Seite 527 und 528:
522 24 Der Poisson’sche Punktproz
- Seite 529 und 530:
524 24 Der Poisson’sche Punktproz
- Seite 531 und 532:
25 Das Itô-Integral Das Itô-Integ
- Seite 533 und 534:
25.1 Das Itô-Integral bezüglich d
- Seite 535 und 536:
25.1 Das Itô-Integral bezüglich d
- Seite 537 und 538:
25.1 Das Itô-Integral bezüglich d
- Seite 539 und 540:
25.2 Itô-Integral bezüglich Diffu
- Seite 541 und 542:
25.2 Itô-Integral bezüglich Diffu
- Seite 543 und 544:
25.3 Die Itô-Formel 539 F (x) =x 2
- Seite 545 und 546:
25.3 Die Itô-Formel 541 Da ε>0 be
- Seite 547 und 548:
ft := lim n→∞ n� � 〈M〉t
- Seite 549 und 550:
25.3 Die Itô-Formel 545 Korollar 2
- Seite 551 und 552:
25.4 Dirichlet-Problem und Brown’
- Seite 553 und 554:
25.5 Rekurrenz und Transienz der Br
- Seite 555 und 556:
26 Stochastische Differentialgleich
- Seite 557 und 558:
26.1 Starke Lösungen 553 Die Exist
- Seite 559 und 560:
Die linke Seite in (26.6) ist aber
- Seite 561 und 562:
und � t Jt := 0 � N b(s, Xs )
- Seite 563 und 564:
1.5 1 0.5 0 26.1 Starke Lösungen 5
- Seite 565 und 566:
26.2 Schwache Lösungen und Marting
- Seite 567 und 568:
26.2 Schwache Lösungen und Marting
- Seite 569 und 570:
Im Folgenden gelte stets: 26.2 Schw
- Seite 571 und 572:
26.3 Eindeutigkeit schwacher Lösun
- Seite 573 und 574:
26.3 Eindeutigkeit schwacher Lösun
- Seite 575 und 576:
3 2 1 0 26.3 Eindeutigkeit schwache
- Seite 577 und 578:
26.3 Eindeutigkeit schwacher Lösun
- Seite 579 und 580:
Literatur 1. M. Aizenman, H. Kesten
- Seite 581 und 582:
Literatur 577 37. R. M. Dudley. Rea
- Seite 583 und 584:
Literatur 579 80. Jürgen Jost. Par
- Seite 585 und 586:
Literatur 581 123. Jim Pitman und M
- Seite 587 und 588:
Notation A Indikatorfunktion der Me
- Seite 589 und 590:
μ ⊥ ν μist singulär bezüglic
- Seite 591 und 592:
Glossar englischer Ausdrücke a.a.
- Seite 593 und 594:
Namensregister Banach, Stefan, 1892
- Seite 595 und 596:
Prohorov, Yurij Vasil’evich (Proh
- Seite 597 und 598:
594 Sachregister Cesàro-Limes 62 C
- Seite 599 und 600:
596 Sachregister -Itô-Formel - - m
- Seite 601 und 602:
598 Sachregister Moran-Modell 343 d
- Seite 603 und 604:
600 Sachregister - terminale 61, 22
- Seite 605:
602 Sachregister Wählermodell 216