- Seite 1 und 2:
Prof. Dr. May-Britt Kallenrode Fach
- Seite 3 und 4:
ii Survival Comfort Extreme 1. Vekt
- Seite 5 und 6:
iv Darstellung ist mehr auf Rechent
- Seite 7 und 8:
Selbständiges Arbeiten Great thing
- Seite 9 und 10:
viii Abbildung 2: Bei der Suche nac
- Seite 11 und 12:
Inhaltsübersicht 1 Vektoren 1 1.1
- Seite 13 und 14:
xii INHALTSÜBERSICHT 12 Statistik
- Seite 15 und 16:
xiv INHALTSVERZEICHNIS Was ist ein
- Seite 17 und 18:
xvi INHALTSVERZEICHNIS 3.7 MatLab:
- Seite 19 und 20:
xviii INHALTSVERZEICHNIS 6.5 Schnee
- Seite 21 und 22:
xx INHALTSVERZEICHNIS Rechenregeln
- Seite 23 und 24:
xxii INHALTSVERZEICHNIS 11.6.5 Drei
- Seite 25 und 26:
0 INHALTSVERZEICHNIS C Erste Hilfe
- Seite 27 und 28:
2 KAPITEL 1. VEKTOREN Abbildung 1.1
- Seite 29 und 30:
4 KAPITEL 1. VEKTOREN 1.2 Grundlage
- Seite 31 und 32:
6 KAPITEL 1. VEKTOREN Abbildung 1.3
- Seite 33 und 34:
8 KAPITEL 1. VEKTOREN • das Assoz
- Seite 35 und 36:
10 KAPITEL 1. VEKTOREN Tabelle 1.1:
- Seite 37 und 38:
12 KAPITEL 1. VEKTOREN Abbildung 1.
- Seite 39 und 40:
14 KAPITEL 1. VEKTOREN 1.4.1 Skalar
- Seite 41 und 42:
16 KAPITEL 1. VEKTOREN ✻ (⃗a ×
- Seite 43 und 44:
18 KAPITEL 1. VEKTOREN Abbildung 1.
- Seite 45 und 46:
20 KAPITEL 1. VEKTOREN Für die Ric
- Seite 47 und 48:
22 KAPITEL 1. VEKTOREN Abbildung 1.
- Seite 49 und 50:
24 KAPITEL 1. VEKTOREN Abbildung 1.
- Seite 51 und 52:
26 KAPITEL 1. VEKTOREN für den Zus
- Seite 53 und 54:
28 KAPITEL 1. VEKTOREN Abbildung 1.
- Seite 55 und 56:
30 KAPITEL 1. VEKTOREN Was ist ein
- Seite 57 und 58:
32 KAPITEL 1. VEKTOREN sind. Also s
- Seite 59 und 60:
34 KAPITEL 1. VEKTOREN § 162 Alle
- Seite 61 und 62: 36 KAPITEL 1. VEKTOREN § 170 Der A
- Seite 63 und 64: 38 KAPITEL 1. VEKTOREN Die für ein
- Seite 65 und 66: 40 KAPITEL 1. VEKTOREN § 185 War d
- Seite 67 und 68: 42 KAPITEL 1. VEKTOREN 1.7.3 Andere
- Seite 69 und 70: 44 KAPITEL 1. VEKTOREN Kontrollfrag
- Seite 71 und 72: 46 KAPITEL 1. VEKTOREN Aufgabe 6 Ü
- Seite 73 und 74: 48 KAPITEL 1. VEKTOREN Literatur §
- Seite 75 und 76: 50 KAPITEL 2. FOLGEN UND REIHEN Abb
- Seite 77 und 78: 52 KAPITEL 2. FOLGEN UND REIHEN Abb
- Seite 79 und 80: 54 KAPITEL 2. FOLGEN UND REIHEN neg
- Seite 81 und 82: 56 KAPITEL 2. FOLGEN UND REIHEN Kon
- Seite 83 und 84: 58 KAPITEL 2. FOLGEN UND REIHEN Abb
- Seite 85 und 86: 60 KAPITEL 2. FOLGEN UND REIHEN §
- Seite 87 und 88: 62 KAPITEL 2. FOLGEN UND REIHEN •
- Seite 89 und 90: 64 KAPITEL 2. FOLGEN UND REIHEN Die
- Seite 91 und 92: 66 KAPITEL 2. FOLGEN UND REIHEN Abb
- Seite 93 und 94: 68 KAPITEL 2. FOLGEN UND REIHEN Abb
- Seite 95 und 96: 70 KAPITEL 2. FOLGEN UND REIHEN §
- Seite 97 und 98: 72 KAPITEL 2. FOLGEN UND REIHEN Abb
- Seite 99 und 100: 74 KAPITEL 2. FOLGEN UND REIHEN For
- Seite 101 und 102: 76 KAPITEL 2. FOLGEN UND REIHEN §
- Seite 103 und 104: 78 KAPITEL 2. FOLGEN UND REIHEN f n
- Seite 105 und 106: Kapitel 3 Funktionen Wir suchen nac
- Seite 107 und 108: 82 KAPITEL 3. FUNKTIONEN § 320 Ein
- Seite 109 und 110: 84 KAPITEL 3. FUNKTIONEN Abbildung
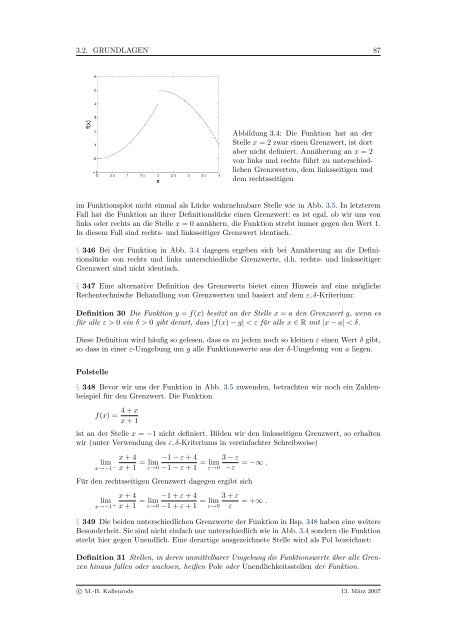
- Seite 111: 86 KAPITEL 3. FUNKTIONEN § 340 Ist
- Seite 115 und 116: 90 KAPITEL 3. FUNKTIONEN Jede Kompo
- Seite 117 und 118: 92 KAPITEL 3. FUNKTIONEN Abbildung
- Seite 119 und 120: 94 KAPITEL 3. FUNKTIONEN Abbildung
- Seite 121 und 122: 96 KAPITEL 3. FUNKTIONEN Abbildung
- Seite 123 und 124: 98 KAPITEL 3. FUNKTIONEN y = mx und
- Seite 125 und 126: 100 KAPITEL 3. FUNKTIONEN Auflösen
- Seite 127 und 128: 102 KAPITEL 3. FUNKTIONEN Abbildung
- Seite 129 und 130: 104 KAPITEL 3. FUNKTIONEN Abbildung
- Seite 131 und 132: 106 KAPITEL 3. FUNKTIONEN Abbildung
- Seite 133 und 134: 108 KAPITEL 3. FUNKTIONEN 10 120 10
- Seite 135 und 136: 110 KAPITEL 3. FUNKTIONEN § 438 Ei
- Seite 137 und 138: 112 KAPITEL 3. FUNKTIONEN Abbildung
- Seite 139 und 140: 114 KAPITEL 3. FUNKTIONEN Abbildung
- Seite 141 und 142: 116 KAPITEL 3. FUNKTIONEN Abbildung
- Seite 143 und 144: 118 KAPITEL 3. FUNKTIONEN Kontrollf
- Seite 145 und 146: 120 KAPITEL 3. FUNKTIONEN Aufgaben
- Seite 147 und 148: 122 KAPITEL 4. DIFFERENTIALRECHNUNG
- Seite 149 und 150: 124 KAPITEL 4. DIFFERENTIALRECHNUNG
- Seite 151 und 152: 126 KAPITEL 4. DIFFERENTIALRECHNUNG
- Seite 153 und 154: 128 KAPITEL 4. DIFFERENTIALRECHNUNG
- Seite 155 und 156: 130 KAPITEL 4. DIFFERENTIALRECHNUNG
- Seite 157 und 158: 132 KAPITEL 4. DIFFERENTIALRECHNUNG
- Seite 159 und 160: 134 KAPITEL 4. DIFFERENTIALRECHNUNG
- Seite 161 und 162: 136 KAPITEL 4. DIFFERENTIALRECHNUNG
- Seite 163 und 164:
138 KAPITEL 4. DIFFERENTIALRECHNUNG
- Seite 165 und 166:
140 KAPITEL 4. DIFFERENTIALRECHNUNG
- Seite 167 und 168:
142 KAPITEL 4. DIFFERENTIALRECHNUNG
- Seite 169 und 170:
144 KAPITEL 4. DIFFERENTIALRECHNUNG
- Seite 171 und 172:
146 KAPITEL 4. DIFFERENTIALRECHNUNG
- Seite 173 und 174:
148 KAPITEL 4. DIFFERENTIALRECHNUNG
- Seite 175 und 176:
150 KAPITEL 4. DIFFERENTIALRECHNUNG
- Seite 177 und 178:
152 KAPITEL 4. DIFFERENTIALRECHNUNG
- Seite 179 und 180:
154 KAPITEL 4. DIFFERENTIALRECHNUNG
- Seite 181 und 182:
156 KAPITEL 4. DIFFERENTIALRECHNUNG
- Seite 183 und 184:
158 KAPITEL 4. DIFFERENTIALRECHNUNG
- Seite 185 und 186:
160 KAPITEL 4. DIFFERENTIALRECHNUNG
- Seite 187 und 188:
162 KAPITEL 4. DIFFERENTIALRECHNUNG
- Seite 189 und 190:
Kapitel 5 Integration Discovery con
- Seite 191 und 192:
166 KAPITEL 5. INTEGRATION Abbildun
- Seite 193 und 194:
168 KAPITEL 5. INTEGRATION § 650 N
- Seite 195 und 196:
170 KAPITEL 5. INTEGRATION Fallen d
- Seite 197 und 198:
172 KAPITEL 5. INTEGRATION Integrat
- Seite 199 und 200:
174 KAPITEL 5. INTEGRATION parallel
- Seite 201 und 202:
176 KAPITEL 5. INTEGRATION Abbildun
- Seite 203 und 204:
178 KAPITEL 5. INTEGRATION bestimme
- Seite 205 und 206:
180 KAPITEL 5. INTEGRATION Dreifach
- Seite 207 und 208:
182 KAPITEL 5. INTEGRATION als ∫
- Seite 209 und 210:
184 KAPITEL 5. INTEGRATION verricht
- Seite 211 und 212:
186 KAPITEL 5. INTEGRATION 5.5.2 Tr
- Seite 213 und 214:
188 KAPITEL 5. INTEGRATION Abbildun
- Seite 215 und 216:
190 KAPITEL 5. INTEGRATION cumsum c
- Seite 217 und 218:
192 KAPITEL 5. INTEGRATION Abbildun
- Seite 219 und 220:
194 KAPITEL 5. INTEGRATION Abbildun
- Seite 221 und 222:
196 KAPITEL 5. INTEGRATION Frage 60
- Seite 223 und 224:
198 KAPITEL 5. INTEGRATION Aufgaben
- Seite 225 und 226:
200 KAPITEL 6. KOMPLEXE ZAHLEN da m
- Seite 227 und 228:
202 KAPITEL 6. KOMPLEXE ZAHLEN Abbi
- Seite 229 und 230:
204 KAPITEL 6. KOMPLEXE ZAHLEN Abbi
- Seite 231 und 232:
206 KAPITEL 6. KOMPLEXE ZAHLEN § 7
- Seite 233 und 234:
208 KAPITEL 6. KOMPLEXE ZAHLEN Abbi
- Seite 235 und 236:
210 KAPITEL 6. KOMPLEXE ZAHLEN Die
- Seite 237 und 238:
212 KAPITEL 6. KOMPLEXE ZAHLEN § 8
- Seite 239 und 240:
214 KAPITEL 6. KOMPLEXE ZAHLEN Funk
- Seite 241 und 242:
216 KAPITEL 6. KOMPLEXE ZAHLEN Abbi
- Seite 243 und 244:
218 KAPITEL 6. KOMPLEXE ZAHLEN Abbi
- Seite 245 und 246:
220 KAPITEL 6. KOMPLEXE ZAHLEN Abbi
- Seite 247 und 248:
222 KAPITEL 6. KOMPLEXE ZAHLEN Abbi
- Seite 249 und 250:
224 KAPITEL 6. KOMPLEXE ZAHLEN Kont
- Seite 251 und 252:
226 KAPITEL 6. KOMPLEXE ZAHLEN Math
- Seite 253 und 254:
Kapitel 7 Gewöhnliche Differential
- Seite 255 und 256:
230 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 257 und 258:
232 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 259 und 260:
234 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 261 und 262:
236 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 263 und 264:
238 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 265 und 266:
240 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 267 und 268:
242 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 269 und 270:
244 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 271 und 272:
246 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 273 und 274:
248 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 275 und 276:
250 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 277 und 278:
252 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 279 und 280:
254 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 281 und 282:
256 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 283 und 284:
258 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 285 und 286:
260 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 287 und 288:
262 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 289 und 290:
264 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 291 und 292:
266 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 293 und 294:
268 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 295 und 296:
270 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 297 und 298:
272 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 299 und 300:
274 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 301 und 302:
276 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 303 und 304:
278 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 305 und 306:
280 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 307 und 308:
282 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 309 und 310:
284 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 311 und 312:
286 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 313 und 314:
288 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 315 und 316:
290 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 317 und 318:
292 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 319 und 320:
294 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 321 und 322:
296 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 323 und 324:
298 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 325 und 326:
300 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 327 und 328:
302 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 329 und 330:
304 KAPITEL 7. GEWÖHNLICHE DIFFERE
- Seite 331 und 332:
306 KAPITEL 8. MATRIZEN Zusammenhan
- Seite 333 und 334:
308 KAPITEL 8. MATRIZEN Abbildung 8
- Seite 335 und 336:
310 KAPITEL 8. MATRIZEN 8.2.1 Grund
- Seite 337 und 338:
312 KAPITEL 8. MATRIZEN § 1156 Als
- Seite 339 und 340:
314 KAPITEL 8. MATRIZEN Jeder Kompo
- Seite 341 und 342:
316 KAPITEL 8. MATRIZEN 1 √ (|↑
- Seite 343 und 344:
318 KAPITEL 8. MATRIZEN Transponier
- Seite 345 und 346:
320 KAPITEL 8. MATRIZEN = (a 11 a 2
- Seite 347 und 348:
322 KAPITEL 8. MATRIZEN § 1201 Die
- Seite 349 und 350:
324 KAPITEL 8. MATRIZEN § 1214 Eig
- Seite 351 und 352:
326 KAPITEL 8. MATRIZEN 8.3 Mathema
- Seite 353 und 354:
328 KAPITEL 8. MATRIZEN § 1232 Zum
- Seite 355 und 356:
330 KAPITEL 8. MATRIZEN Das ist sel
- Seite 357 und 358:
332 KAPITEL 8. MATRIZEN § 1248 Wen
- Seite 359 und 360:
334 KAPITEL 8. MATRIZEN Abbildung 8
- Seite 361 und 362:
336 KAPITEL 8. MATRIZEN Abbildung 8
- Seite 363 und 364:
338 KAPITEL 8. MATRIZEN Lorentz Tra
- Seite 365 und 366:
340 KAPITEL 8. MATRIZEN Die Deviati
- Seite 367 und 368:
342 KAPITEL 8. MATRIZEN Die Eigenwe
- Seite 369 und 370:
344 KAPITEL 8. MATRIZEN Abbildung 8
- Seite 371 und 372:
346 KAPITEL 8. MATRIZEN Abbildung 8
- Seite 373 und 374:
348 KAPITEL 8. MATRIZEN Kontrollfra
- Seite 375 und 376:
350 KAPITEL 8. MATRIZEN Mathematisc
- Seite 377 und 378:
Kapitel 9 Verallgemeinerte Funktion
- Seite 379 und 380:
354 KAPITEL 9. VERALLGEMEINERTE FUN
- Seite 381 und 382:
356 KAPITEL 9. VERALLGEMEINERTE FUN
- Seite 383 und 384:
358 KAPITEL 9. VERALLGEMEINERTE FUN
- Seite 385 und 386:
360 KAPITEL 9. VERALLGEMEINERTE FUN
- Seite 387 und 388:
362 KAPITEL 9. VERALLGEMEINERTE FUN
- Seite 389 und 390:
364 KAPITEL 9. VERALLGEMEINERTE FUN
- Seite 391 und 392:
366 KAPITEL 9. VERALLGEMEINERTE FUN
- Seite 393 und 394:
Kapitel 10 Vektoranalysis I’ve go
- Seite 395 und 396:
370 KAPITEL 10. VEKTORANALYSIS Abbi
- Seite 397 und 398:
372 KAPITEL 10. VEKTORANALYSIS sind
- Seite 399 und 400:
374 KAPITEL 10. VEKTORANALYSIS Abbi
- Seite 401 und 402:
376 KAPITEL 10. VEKTORANALYSIS § 1
- Seite 403 und 404:
378 KAPITEL 10. VEKTORANALYSIS und
- Seite 405 und 406:
380 KAPITEL 10. VEKTORANALYSIS Abbi
- Seite 407 und 408:
382 KAPITEL 10. VEKTORANALYSIS ist
- Seite 409 und 410:
384 KAPITEL 10. VEKTORANALYSIS Abbi
- Seite 411 und 412:
386 KAPITEL 10. VEKTORANALYSIS Abbi
- Seite 413 und 414:
388 KAPITEL 10. VEKTORANALYSIS § 1
- Seite 415 und 416:
390 KAPITEL 10. VEKTORANALYSIS und
- Seite 417 und 418:
392 KAPITEL 10. VEKTORANALYSIS Abbi
- Seite 419 und 420:
394 KAPITEL 10. VEKTORANALYSIS § 1
- Seite 421 und 422:
396 KAPITEL 10. VEKTORANALYSIS Rota
- Seite 423 und 424:
398 KAPITEL 10. VEKTORANALYSIS § 1
- Seite 425 und 426:
400 KAPITEL 10. VEKTORANALYSIS § 1
- Seite 427 und 428:
402 KAPITEL 10. VEKTORANALYSIS Aufg
- Seite 429 und 430:
404 KAPITEL 10. VEKTORANALYSIS Aufg
- Seite 431 und 432:
Kapitel 11 Partielle Differentialgl
- Seite 433 und 434:
408 KAPITEL 11. PARTIELLE DIFFERENT
- Seite 435 und 436:
410 KAPITEL 11. PARTIELLE DIFFERENT
- Seite 437 und 438:
412 KAPITEL 11. PARTIELLE DIFFERENT
- Seite 439 und 440:
414 KAPITEL 11. PARTIELLE DIFFERENT
- Seite 441 und 442:
416 KAPITEL 11. PARTIELLE DIFFERENT
- Seite 443 und 444:
418 KAPITEL 11. PARTIELLE DIFFERENT
- Seite 445 und 446:
420 KAPITEL 11. PARTIELLE DIFFERENT
- Seite 447 und 448:
422 KAPITEL 11. PARTIELLE DIFFERENT
- Seite 449 und 450:
424 KAPITEL 11. PARTIELLE DIFFERENT
- Seite 451 und 452:
426 KAPITEL 11. PARTIELLE DIFFERENT
- Seite 453 und 454:
428 KAPITEL 11. PARTIELLE DIFFERENT
- Seite 455 und 456:
430 KAPITEL 11. PARTIELLE DIFFERENT
- Seite 457 und 458:
432 KAPITEL 11. PARTIELLE DIFFERENT
- Seite 459 und 460:
434 KAPITEL 11. PARTIELLE DIFFERENT
- Seite 461 und 462:
436 KAPITEL 12. STATISTIK 12.1.1 Ko
- Seite 463 und 464:
438 KAPITEL 12. STATISTIK § 1635 B
- Seite 465 und 466:
440 KAPITEL 12. STATISTIK mit der d
- Seite 467 und 468:
442 KAPITEL 12. STATISTIK Abbildung
- Seite 469 und 470:
444 KAPITEL 12. STATISTIK Tabelle 1
- Seite 471 und 472:
446 KAPITEL 12. STATISTIK wird, ist
- Seite 473 und 474:
448 KAPITEL 12. STATISTIK Abbildung
- Seite 475 und 476:
450 KAPITEL 12. STATISTIK Abbildung
- Seite 477 und 478:
452 KAPITEL 12. STATISTIK § 1686 E
- Seite 479 und 480:
454 KAPITEL 12. STATISTIK 12.3.1 In
- Seite 481 und 482:
456 KAPITEL 12. STATISTIK Abbildung
- Seite 483 und 484:
458 KAPITEL 12. STATISTIK die erwar
- Seite 485 und 486:
460 KAPITEL 12. STATISTIK Abbildung
- Seite 487 und 488:
462 KAPITEL 12. STATISTIK Abb. 12.1
- Seite 489 und 490:
464 KAPITEL 12. STATISTIK Tabelle 1
- Seite 491 und 492:
466 KAPITEL 12. STATISTIK Nach Divi
- Seite 493 und 494:
468 KAPITEL 12. STATISTIK Abbildung
- Seite 495 und 496:
470 KAPITEL 12. STATISTIK von (12.3
- Seite 497 und 498:
472 KAPITEL 12. STATISTIK (12.34) i
- Seite 499 und 500:
474 KAPITEL 12. STATISTIK Aufgabe 2
- Seite 501 und 502:
476 KAPITEL 12. STATISTIK Aufgabe 2
- Seite 503 und 504:
Anhang A Nützliches .... ... A.1 F
- Seite 505 und 506:
Anhang B MatLab: The Basics .... ..
- Seite 507 und 508:
482 ANHANG B. MATLAB: THE BASICS §
- Seite 509 und 510:
484 ANHANG B. MATLAB: THE BASICS Be
- Seite 511 und 512:
486 ANHANG B. MATLAB: THE BASICS §
- Seite 513 und 514:
488 ANHANG B. MATLAB: THE BASICS 1.
- Seite 515 und 516:
490 ANHANG B. MATLAB: THE BASICS B.
- Seite 517 und 518:
492 ANHANG B. MATLAB: THE BASICS pi
- Seite 519 und 520:
494 ANHANG B. MATLAB: THE BASICS ab
- Seite 521 und 522:
496 ANHANG B. MATLAB: THE BASICS po
- Seite 523 und 524:
498 ANHANG B. MATLAB: THE BASICS Ma
- Seite 525 und 526:
500 ANHANG B. MATLAB: THE BASICS +
- Seite 527 und 528:
502 ANHANG B. MATLAB: THE BASICS dx
- Seite 529 und 530:
504 ANHANG B. MATLAB: THE BASICS
- Seite 531 und 532:
506 ANHANG B. MATLAB: THE BASICS su
- Seite 533 und 534:
508 ANHANG B. MATLAB: THE BASICS fh
- Seite 535 und 536:
510 ANHANG B. MATLAB: THE BASICS en
- Seite 537 und 538:
512 ANHANG B. MATLAB: THE BASICS [t
- Seite 539 und 540:
514 ANHANG C. ERSTE HILFE n = 0 1 n
- Seite 541 und 542:
516 ANHANG C. ERSTE HILFE Wir ziehe
- Seite 543 und 544:
518 ANHANG C. ERSTE HILFE Beider Qu
- Seite 545 und 546:
520 ANHANG C. ERSTE HILFE Abbildung
- Seite 547 und 548:
522 ANHANG C. ERSTE HILFE schleunig
- Seite 549 und 550:
524 ANHANG C. ERSTE HILFE Ableitung
- Seite 551 und 552:
526 ANHANG C. ERSTE HILFE und damit
- Seite 553 und 554:
528 ANHANG C. ERSTE HILFE Alternati
- Seite 555 und 556:
530 ANHANG C. ERSTE HILFE Abbildung
- Seite 557 und 558:
532 ANHANG C. ERSTE HILFE • die S
- Seite 559 und 560:
534 ANHANG C. ERSTE HILFE Beachten
- Seite 561 und 562:
536 ANHANG C. ERSTE HILFE Abbildung
- Seite 563 und 564:
538 ANHANG C. ERSTE HILFE § 1900 D
- Seite 565 und 566:
540 ANHANG C. ERSTE HILFE Differenz
- Seite 567 und 568:
542 ANHANG C. ERSTE HILFE Aufgabe 3
- Seite 569 und 570:
544 ANHANG C. ERSTE HILFE Aufgabe 3
- Seite 571 und 572:
546 ANHANG D. LÖSUNGEN ZU FRAGEN U
- Seite 573 und 574:
548 ANHANG D. LÖSUNGEN ZU FRAGEN U
- Seite 575 und 576:
550 ANHANG D. LÖSUNGEN ZU FRAGEN U
- Seite 577 und 578:
552 ANHANG D. LÖSUNGEN ZU FRAGEN U
- Seite 579 und 580:
554 ANHANG D. LÖSUNGEN ZU FRAGEN U
- Seite 581 und 582:
Abbildungsverzeichnis 1 Information
- Seite 583 und 584:
558 ABBILDUNGSVERZEICHNIS 6.4 Küst
- Seite 585 und 586:
560 ABBILDUNGSVERZEICHNIS C.5 Stamm
- Seite 587 und 588:
Literaturverzeichnis [1] M. Abramow
- Seite 589 und 590:
564 LITERATURVERZEICHNIS [55] W.H.
- Seite 591 und 592:
566 INDEX grid off, 109 grid on, 10
- Seite 593 und 594:
568 INDEX Blindwiderstand, 208 Boge
- Seite 595 und 596:
570 INDEX Euler Formel, 62, 63, 66,
- Seite 597 und 598:
572 INDEX Funktion, 86 geometrische
- Seite 599 und 600:
574 INDEX MatLab, 43 Kriechfall, 24
- Seite 601 und 602:
576 INDEX parallel, 6 gegensinnig,
- Seite 603 und 604:
578 INDEX gedämpft, 242 gedämpfte
- Seite 605 und 606:
580 INDEX interne, 211 Verschiebung